Real options is the modern approach to capital budgeting. This approach considers the value of the opened options for the decision makers.
The origin of the term "real options" can be attributed to the Prof. Stewart Myers ("Determinants of Capital Borrowing", Journal of Financial Economics, vol.5, 1977), who first identified the fact that many corporate real assets can be viewed as call options.
The real options approach is dynamic in the sense that includes the effect of uncertainty along the time, and what/how/when the relevant real options shall be exercised.
The real options problem can be viewed as a problem of optimization under uncertainty of a real asset (project, firm, land, etc.) given the available options.
Although Black-Scholes-Merton and financial options came first in the
70's, and the mathematical methods are the same, real options approach is
not a mere adaptation of financial options approach.
There are several differences between real options and financial options.
Four examples:
1) for real options sometimes are important to consider the time
to build the underlying asset;
2) real options in general have longer time to expiration than financial
options, sometimes even perpetual real options, as the
case of land.
3) private uncertainties sometimes are very important in
real options models.
4) the decision rule (earlier exercise threshold or
critical value) is much more important in real options applications than
in financial options. By the other side, the "greeks" play no
important role in real options models (although is very important for
financial options).
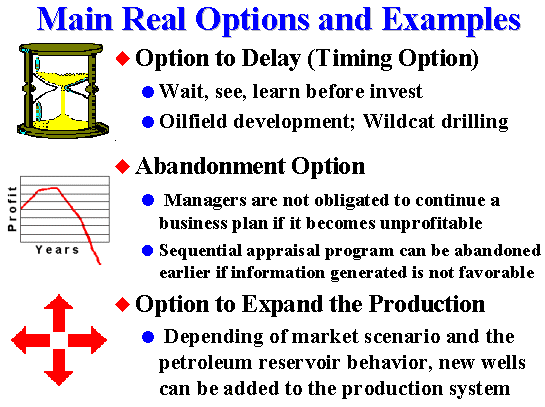
Main types of real options (for a detailed real options classification, see the Trigeorgis' textbook (1996):

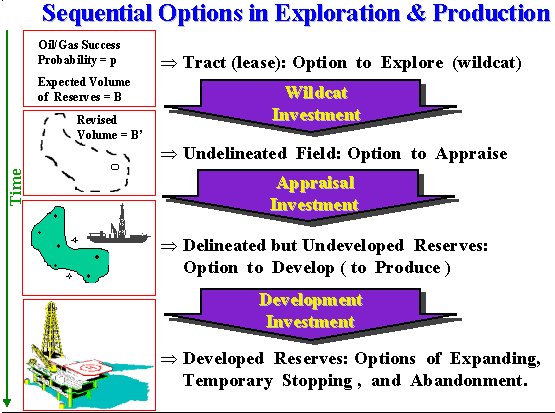
Example of real options: sequential options in exploration and production of petroleum.
There are a controversy if the use of dynamic programming for
optimization under uncertainty can be considered as a part of "real
options" or not.
Some people even say that it is "investment under uncertainty"
or "dynamic programming" , not "real options".
This thinking is too influenced by the Black-Scholes and financial
options. I prefer the original more general concept of Myers, to see the
option like features of the corporate real assets, not the specific
methodology used to solve financial options, even being a breakthrough in
financial and economic theory.
Although the "contingent claims" (arbitrage, risk-free
portfolio) is preferable if the market is complete, for incomplete markets
the use of "dynamic programming" with an exogenous discount rate
is not only a good but a practical tool. Both consider the available
managerial flexibility (the "real options") into a
dynamic framework with uncertainty (see FAQ 5 for a discussion). This
is the essence of real options concept.
As in Dixit & Pindyck (1994), I consider "real options" and
the modern "investment under uncertainty" as synonyms.
So, real options don't need that contingent claims approach to be applicable, neither that the source of uncertainty comes from the market (real options are valuable in the presence of private or technical uncertainty), nor that the Black-Scholes assumptions to be valid. The "real options tool kit" is larger.
In order to characterize a model as a "real options approach",
the important is to see if the model recognize the relevant options
available to the decisors and if the model captures a fair value for these
real options in an environment of uncertainty. For me, real options model
is a maximization of value subject to the uncertainties and given the
(real) options available. As contingent claims, dynamic programming is
just one way to perform this job.
Market values must be used always is possible. But the lack of some
market values doesn't mean that real options approach is not possible.
As Amram & Kulatilaka say, real options "is a way of thinking".
![]()
![]()