FAQ Number 12

Will the Total Volatility of the Model Be Increased if I Add Other Sources of Uncertainty?

Answer: Not necessarily.

The case below was studied in my M.Sc. dissertation. In the problem of a real option F to develop a project with value V and with development cost equal D, so that in case of option exercise the payoff is V - D.
Consider that, in addition to the project value (V) uncertainty represented by the volatility s_V, the investment cost (D) is also uncertain with volatility s_D. Assume that both (V and D) follow correlated geometric Brownian motions.

What happen if we start to add cost uncertainty into this model? The answer depends of the correlation and of each individual volatility.

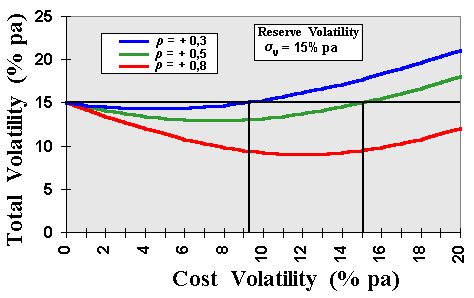
The chart below shows three different correlations between the two processes. The correlation is expected to be positive for the general case.

The chart above shows that for these positive correlation and for cost volatility lower than ~9% p.a., the addition of cost volatility reduces the total uncertainty of the process!
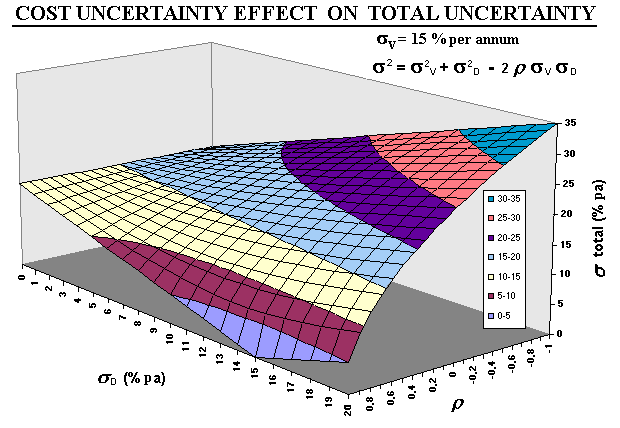
Only for independent (r =0) or for negative correlation, that the cost uncertainty will increase the total uncertainty (see the 3D chart below). However, in most cases the correlation is positive as in the picture above.

The 3D chart shows a whole range of correlations. The equation for the total uncertainty is also displayed in the picture.

For the equation displayed in the chart for the "total uncertainty", see for example:

• McDonald, R. & D. Siegel (1986): "The Value of Waiting to Invest" Quarterly Journal of Economics, November 1986, pp.707-727 (see the paragraph after equation 5)
• Dixit & Pindyck (1994), Investment under Uncertainty, chapter 6, eq.29 (compare the first term with eq.6, for example)
• Carr, P. (1995): "The Valuation of American Exchange Options with Application to Real Options" Real Options in Capital Investments: Models, Strategies, and Aplications - Ed. by L. Trigeorgis, Praeger Publisher, Westport, Conn., 1995, pp.109-120 (see p.111, after eq.6.2)
• Kensinger, J. (1987): "Adding the Value of Active Management into the Capital Budgeting Equation" Midland Corporate Finance Journal, vol.5, no 1, Spring 1987, pp.31-42 (see appendix)

This case is simple thanks to the property of homogeneity of degree one of the differential equation, so that is possible to work with the ratio V/D for the underlying asset (with its "total volatility") and the ratio F/D for the option.
Homogeneity of degree one means that F(V/D, D/D) = (1/D) F(V, D), and it permits to use V/D in the maximization problem. The threshold (V/D)* is homogeneous of degree zero in V and D, see the classical paper of McDonald & Siegel (1986, p.713).