Instructions and Features on Static and Animated Charts

Introduction

The sensitivity analysis for American call option on a continuous dividend yield paying asset, is performed using both static and animated charts.

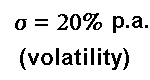
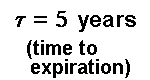
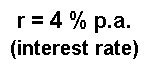
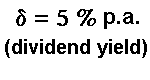
The study of this kind of financial option is very important for real investment opportunities, because the irreversible investment expenditure on projects that generates continuous cash-flow is like a call option: in general is possible to wait and see for new informations and better conditions, and the waiting policy is optimal if the project is not deep in the money.

The American call analogy is one of best models to start real options applications, due the simplicity of this framework, while remain theoretically sound (see a note about the model). You need only to know the present value of the operating project (revenue less operational cost and taxes, all in present values), the (after-tax) present value of the investment, the interest rate, the dividend yield (annual cash flow divided by the operating project value, in general) and the time to expiration of the investment opportunity. With these variables you can get the value of the opportunity (option) to invest in real assets (projects).
In petroleum case, due the reservoir depletion, the dividend yield should be calculated in a less trivial way. See the demonstration for the petroleum case in the tutorial page.

The analysis are performed starting from a Base Case which assumes the following values:

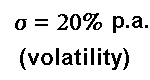
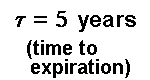
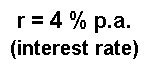
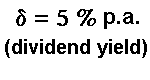
The static graphs show the sensitivity analysis in a conventional way, but using hyperlinks to get easily the specific chart for a specific value. There are about 140 static charts to choose.

The dynamic charts presents the sensitivity analysis in a less conventional way, like a small movie where one line from the chart moves by changing continuously of one parameter from the Base Case. This issue is performed simply using animated-GIF method, one interesting visual facility from Web-Internet environment. There are 7 dynamic charts.

For both static and dynamic charts, this site presents two types of charts: charts about the option value and charts about thresholds for earlier option exercise (free-boundary).

Option Value Charts

The option value charts from the sensitivity analysis looks like the following graph value:

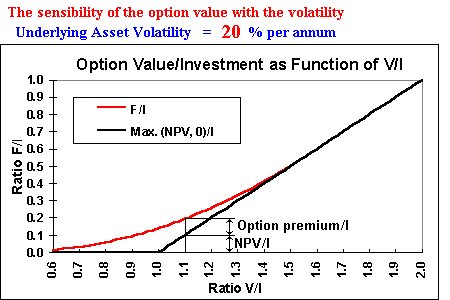
This kind of chart shows the option value F against the underlying asset value V. These values are presented in the charts in normalized terms, that is, are values per unit of investment I (or per unit of exercise price of the option) for didatic reasons: if the ration V/I is more than 1, the option is in the money, and if this ratio is less than 1 the option is out of money, so is easier to see in the chart how deep or out of money is the option.
The option value is also per unit of investment (or per unit of exercise price). Of course, to obtain the total option value F, just multiplies F/I by the investment (exercise price) I.
The use of these ratios is also useful to analyse investment uncertainty effect.

There are two lines in the chart:
(a) the value at the expiration (the "now or never" value), the two black straight lines which represent the maximum between the payoff and zero, or in others words, between NPV and zero, where NPV ( NPV = V - I ) means net present value. I use the term NPV in order to remember the analogy with real investments, which is the main goal of this analysis.
(b) the option value (the red curve), which values more than the expiration value except when the option is sufficiently "deep in the money" (when F = NPV).
The point where the option curve smooth pasting the straight line from the payoff (the NPV line) is the optimal level for early exercise of the option. At this point, the early exercise is optimal, because the net waiting value (the option premium) is zero. This chart shows the NPV and the option value F (both per unit of investment), for the underlying asset value of 1.1 times the exercise price (V/I = 1.1). Although the option is in the money, the net waiting value (the option premium) is positive, so the option is not sufficiently deep in the money to be exercised.

Besides the volatility (showed in the graph-example above), also are performed sensitivity analysis for the other parameters (dividend yield, interest rate, time to expiration).

Threshold Charts

The following chart shows the early exercise line, that is, the threshold curve (also known as free-boundary by mathematicians). This line represents the decision rule for the early option exercise (and is analog to optimal real investment problem).

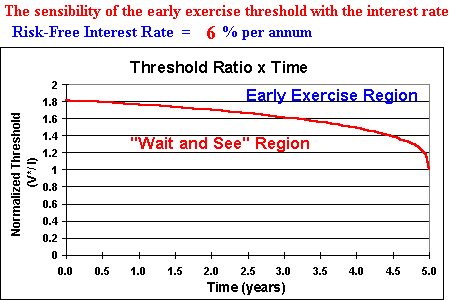
Also in this kind of chart the threshold V* is normalized by the investment value (or the exercise price) I, so the Y axis shows the ratio V*/I.
For the case of 5 years to expiration, the chart shows that the underlying asset value needs to reach more than 80% above the investment value, in order to be optimal the immediate exercise of this option. In order words, the option is sufficiently deep in the money only for V*/I > 1.8 if there are 5 years to expiration (and with the parameters values of the example).
In real investment decisions, one threshold 80% above the project value means that the traditional NPV rule (invest if VPL > 0) is not only wrong, it's very wrong (investment decision too far from the optimal investment decision).

The region under the threshold line is the "wait and see" region (the option values more live than dead), whereas above the line is the "immediate investment" region (where is optimal "to kill" the option, exercising the option).
At the expiration (in the end of the fifth year), the threshold ratio is 1, so the NPV rule holds in this case. In this model, the NPV rule holds only in the now or never case and when the option is sufficiently deep in the money.

At this point is useful to point that there are some differences between the financial and real options, which is necessary to take into consideration. One is the expiration time: in real options this time is frequently more than one or two years, whereas in financial option case this time is shorter (the typical is two quarters, although there are longer contracts, e.g. traded options on crude oil with three years length). In petroleum offshore leases, the typical time is 5 to 10 years, and even more in the case of patents rights (e.g. 20 years in Brazil). So, the presented charts are showing time to expiration from 10 years to zero (with several intermediate values).
See others differences between real and financial options in the tutorials page.

Back to Site Contents

Footnotes

American-call Option

An American call option gives the holder the right (not the obligation) to buy the underlying asset in any instant up to the expiration date, for a certain exercise price. The underlying asset can be a stock, a future contract, a foreign currency, etc.
For real options, the underlying asset is the producing project V, that is the net present revenue less the net present operational and taxes costs.

Deep in the Money Project

Even with positive net present value (NPV > 0), the wait and see policy can be optimal. In order to make an optimal irreversible investment, the project need to be sufficiently profitable or deep in the money.
For deep in the money projects, the cost of delay is equal or higher than the benefit to wait for better informations. The benefit of waiting is higher as higher is the uncertainty. The cost of delay is higher as higher is the cash-flow stream (dividend yield) that is postponed with the waiting policy.
See the picture the cost-benefit balance of waiting
Of course there are other parameters which play an important role in this caracterization, such as the timing freedom (time to expiration) and the interest rate. These features are presented in this sensitivity analysis.
American options framework tells when the project is deep in the money, or in other words, the threshold value after which the immediate investment is the optimal policy. In this sensitivity analysis, several threshold charts are presented.
Thresholds are much more important in real options than in financial options, however the delta hedge value (and others Greeks) is much more important in financial options than in real options.

A Note About the Model

In my real options classes, I start with discrete time model, using binomial model in order to develop the student intuition. After this I present the continuous time model as a generalization of the previous discrete time and the American call analogy as powerful practical tool.
Of course there are much more sophisticated models than American call analogy. For example:

models with more complex stochastic processes, such as mean-reversion or jump-Poisson + continuous process, instead the lognormality of the geometric Brownian, sometimes fits better with the underlying asset oscillations;
models allowing the interest rate and/or dividend yield, etc. to be also stochastic (multiple factors models);
models considerating options interactions, like the model of hysteresis (economic effect from entry & exit under uncertainty, see Dixit & Pindyck chapter 7), which there is a call over an underlying asset which is a project + put option (option to abandon), or in other words, a compound option;
interaction with technical uncertainty, which incentives the sequential investment;
interaction with strategic issues, like the "war of attrition" (see my "option-game" slides), or imperfect competition preemption, etc.

But these issues can be view like extensions/sophistication from our simpler American option analogy model, so learning this model is very convenient as first step on real option praxis, providing a good general understanding of real options problems and developing the intuition before to try more complex issues.

Time to Expiration Estimative

The time to expiration can be set by objective legislation (as in petroleum and mineral concessions and patent development projects) or by an estimation of competitors entry timing (if that entry destroys the opportunity, otherwise can be view as perpetual opportunity to invest or a long lived option).
See the discussion of the estimative of time to expiration due the competitor's entry, in the Kester's classic paper (Harvard Business Review, n. 62, March-April 1984, pp.153-160).

In the perfect competitive market situation, Leahy (Quarterly Journal of Economics, 1993, pp.1105-1133) proved the coincidence between a monopoly firm's option-value thresholds (perpetual option) and a competitive firm's free entry threshold.
See a discussion of this remarkable result in the Dixit & Pindyck book (chapter 8).

Cost Uncertainty

The use of the ratios (V/I and F/I) eases the treatment the effect from investment cost uncertainty on the decision rule and option value: due to the differential equation of the option value to be homogeneous of degree one with the investment, is possible to use the same approach of the American option valuation by writing the ratios F/I and V/I for the differential equation, and using the total volatility (volatility of the ratio V/I) instead the alone volatility of V as before.
See the total volatility charts: 3D chart with the equation and the 2D chart for positive correlation.
The total volatility has major impact on the investment decision rule (threshold).

Back to Site Contents