The main goal of these bibliographical pages is to set
a brief thematic review of papers and books. The theme of this review is
the subject of option games, a combination of real options with game
theory.
There are others bibliographical reviews in this web site, see the page
Bibliography by Subjects (with a large review
of Dixit & Pindyck book, and more 5 books or books chapters reviews),
which became archives for the thematic reviews.
This page is dedicated for option-games models. It starts with five reviews, three from articles and two from books chapters. Moreover, in the ending of this page are suggested others articles related with option-games (with a promise to review in a future issue).
Others Important Option Games Articles for Future Review
1) Dixit &
Pindyck
Dixit, A.K. & R.S. Pindyck (1994): "Investment under
Uncertainty"
Princeton University Press, Princeton, N.J., 1994
In chapter 9, section 3, they analyze the imperfect-competition case (duopoly) using option-game approach in continuous time, but for a simple case of perpetual option, and without incomplete information. However they get an analytic solution for the thresholds and values of both leader and follower! The game is a preemption game, with two equilibria by permuting the roles of leader and follower of the two players.
In this model the authors apply other tool from the stochastic calculus arsenal: the expected first hitting time (for details about the concept, see the page about the features of the Timing (Excel software)) in order to calculate player's payoffs.
2) Lambrecht &
Perraudin (a)
Lambrecht, B. & W. Perraudin (1994): "Option Games"
Working Paper, Cambridge University, and CEPR (UK), August
1994, 17 pp.
In "Option Games", the authors analyze a
duopoly, with American put options as payoffs, where the exercise price
are costs of transactions known only by each player (incomplete
information) and the put-threshold is raised because there is an advantage
to act first (preemption game). They calculate the payoff using the
expected first time that the stochastic variable hits the threshold (this
is done in Dixit & Pindyck, too), for each player (minus the
intersection of players’ common scenarios).
The other agent threshold conditional distribution of probabilities is
updated using a method that is similar to "distributional strategies
approach", finding the optimal using standard Laplace maximization,
and derive the condition for the existence of the Nash equilibria.
They provide an example of the model for the "optimal" insider
trading, when there are more than one investor with the inside
information.
3) Lambrecht &
Perraudin (b)
Lambrecht, B. & W. Perraudin (1996): "Real Option and
Preemption"
Working Paper, Cambridge University, Birkbeck College
(London) and CEPR, 35pp.
In "Real Option and Preemption", they focus on preemption game, perpetual option, and incomplete information about the other agent threshold. They simplify the problem considering that after the first entry the other agent loses the investment opportunity. The solution is analytic, and using the notation of our site, the threshold for a perpetual option (V*, where V is the operating project value) is modified (see the Dixit & Pindyck book, p.142, eq.14, for the threshold of the perpetual option to invest) incorporating the "hazard rate" into the equation:
V* =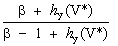 
I
Where b is the
positive (and higher than one) characteristic root of the differential
equation, Y is the other player (competitor), hy(V*)
is the Y’s hazard rate. By adding the hazard rate in this equation,
the threshold decreases (in limit to the Marshallian level). If the hazard
rate is zero, the problem reduces to the traditional timing option
(without game). This solution is valid for preemption game, perpetual
option and for zero "follower payoff".
For the problem of the waiting game, finite option, and lower but non-zero
"loser of the game" payoff (as in the petroleum drilling game,
the SPE paper presented in this site), is not easy to adapt this elegant
solution.
They find this solution with the equilibrium condition similar to the
condition adopted in the drilling game paper (indifference between to
invest and to wait), but they use this condition together with the
smooth-pasting (or alternatively the Lagrangian condition) and the others
boundary conditions (of the stochastic differential equation). This way
perhaps is a good path for the drilling game in continuous time, but the
Bayesian updating remains a bit problem due the finite option with
declining threshold curve. Thus a further research is necessary in order
to use these ideas for a fully dynamic continuous time drilling model or
other finite option model.
4) Trigeorgis
Trigeorgis, L. (1996): "Real Options - Managerial Flexibility and
Strategy in Resource Allocation"
MIT Press, Cambridge, MA, 1996, 427 pp.
In the chapter 9 of his textbook, Trigeorgis also
studied the preemption game combined with option approach. The idea is
incorporate the preemption effect on the threshold, reducing it by adding
a positive value in the dividend yield parameter. This parameter has large
influence on the threshold (see a typical chart, for example, in Dixit &
Pindyck, p.157, Fig.5.6).
This additional dividend is a "competitive dividend"
which is lost for the owner of the real option, in analogy with the cash
dividend which is lost for the owner of a call option on a dividend-paying
stock (or the convenience yield which is lost by the owner of a future
contract of a commodity).
If in the preemption game is added a positive value on the dividend yield, for the opposite timing game, the war of attrition, one idea is decrease the dividend yield, by adding a negative dividend due the extra waiting effect of the game. The challenge is how to incorporate this complex analysis, including considerations of the Bayesian-Nash equilibrium, in the dividend yield expression.
Trigeorgis also develops a game tree analysis, similar
to the presented in the SPE option-game model, he also founds the
equilibria set of strategies by backward induction and using binomial
valuation.
He analyzes both cases, the preemption game and the waiting game. In this
last case (p.298), the problem is analogous of that here analyzed (there,
a R&D investment of a firm results in a cost benefit for who spend in
R&D, but also for the competitor). However, their analysis is more
simplified, for example not considering the incomplete information
subject, and so not updating the probabilities of the other player, using
the information obtained with each move.
5) Grenadier
Grenadier, S.R. (1996): "Strategic Exercise of Options: Development
Cascades and Overbuilding in Real Estate Markets"
Journal of Finance, vol.51, no 5, December 1996, pp.1653-1679
Grenadier develops an option-game model for real estate
investment timing, again one preemption game.
Preemption by a competitor explains the exercise of the call option to
develop a real estate in declining demand. This paper considers the time
to build (ranging from 6 months to more than 5 years) effect on option
value.
He develops a two builders subgame perfect equilibria, finding a pair of
symmetric Markovian exercise strategies. The option exercise is optimal
conditional on the other player exercise strategy. There is an infinite
set of equilibria exercise strategies, and he focused on the Pareto
optimal one.
The analysis of a sequential investment option, the "development
cascades", shows that the demand volatility reduces the median time
between investment starts.
1) Caplin, A. &
J. Leahy (1994): "Business as Usual, Market Crashes, and Wisdom After
the Fact"
American Economic Review, vol.84, no 3, June 1994, pp.548-565
2) Smit, H.T.J.
& L.A. Ankum (1993): "A Real Options and Game-Theoretic Approach
to Corporate Investment Strategy under Competition"
Financial Management, Autumn 1993, pp.241-250
3) Kulatilaka,
N. & E.C. Perotti (1997): "Strategic Growth Options"
Working Paper, Boston University & University of Amsterdam,
April 1997, 22 pp. (forthcoming in Management Science).
4) Trigeorgis,
L. (1991): "Antecipated Competitive Entry and Early Preemptive
Investment in Deferrable Projects"
Journal of Economics and Business, May 1991, vol.43, n.2,
pp.143-156
OBS: See also a light paper related to this subject, in Harvard Business
Review, Nov-Dec/97. The article title is "Strategy under Uncertainty"