FAQ Number 3

Where the real options value comes from?
Why real options value is different of the static net present value (NPV)?

Answer with example: the option to expand.

• Suppose a manager embed an option to expand into her project, by a cost of US$ 1 million;
• The static NPV = - 5 million if the option is exercise today, and in future is expected the same negative NPV;
• Spending a million $ for an expected negative NPV: Is the manager becoming crazy?

Uncertainty Over the Expansion Value:
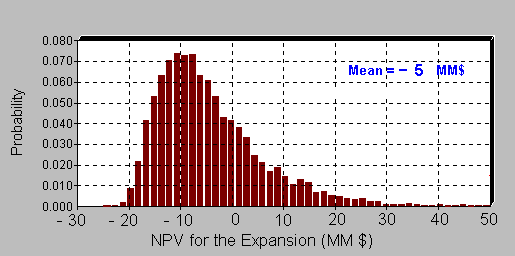
Considering combined uncertainties: in product prices and demand, exercise price of the real option, operational costs, etc., the future value (2 years ahead) of the expansion has an expected value of $ - 5 million. The figure below illustrates that.

The traditional discount cash will not recommend to embed an option to expansion which is expected to be negative.
But the expansion is an option, not an obligation!
Rational managers will not exercise the option to expand @ t = 2 years in case of bad news (negative value), only will exercise the options in case of good news.

• Option will be exercised only if the NPV > 0. So, the unfavorable scenarios will be pruned (for NPV < 0, value = 0);
• The options asymmetry leverage prospect valuation.
  So, Real Option Value = + 5.
  See the "visual equation" below:

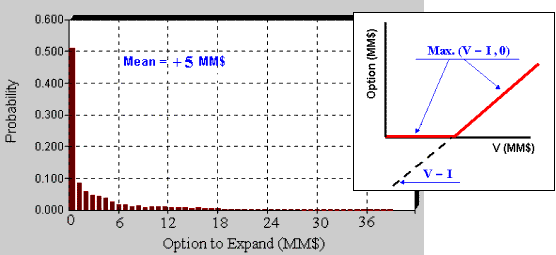
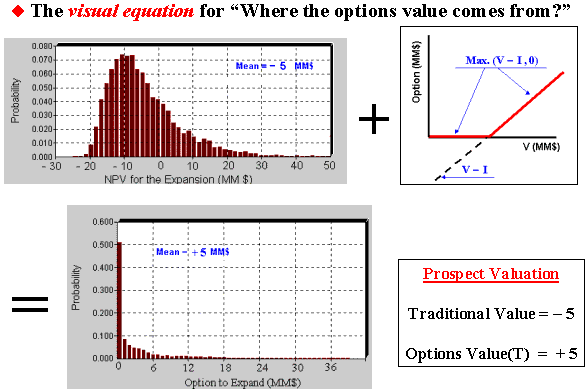
Look the above "equation" and answer: What happen with the option value if the uncertainty is higher (with the same mean)?
Simple: both negative values and positive ones become more spread out. But the negative values doesn't matter because with option a NPV negative become zero, however the upside has a higher value in this case, increasing the option value.
This is an alternative explanation of why uncertainty increases the value of the real option.

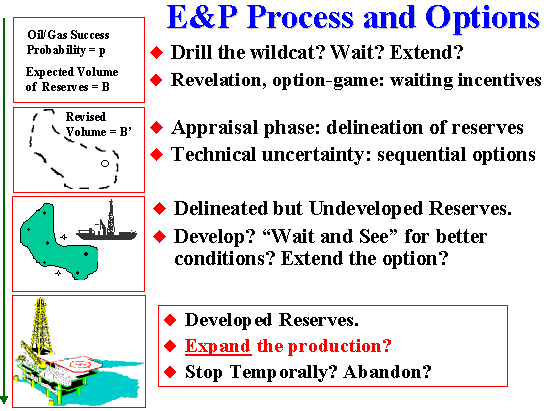
Let us show an example of option to expand the production for a petroleum E&P (exploration & production) case.
The figure below shows the E&P investment as a sequential option process. See in particular the last phase (producing asset phase).

Analyzing a large ultra-deepwater project in Campos Basin, Brazil, we faced two problems:

• Remaining technical uncertainty of reservoirs is still important. In this specific case, the better way to solve the uncertainty is by looking the production profile instead drilling additional appraisal wells
• In the preliminary development plan, some wells presented both reservoir risk and small NPV.
• Some wells with small positive NPV (not “deep-in-the-money”) and others even with negative NPV;
• Depending of the initial production information, some wells can be not necessary.

Solution: leave these wells as optional wells

Allocate only a small but important investment to permit a fast and low cost future integration of these wells, depending of both market (oil prices, costs) and the production profile response. This cost comprises the cost to leave stand-by both area and load in the production platform for the optional new wells, and a subsea lay-out so that permits an easy integration with the existing system in case to exercise some of the option to drill these optional wells.
So the development project is not optimized statically, it is optimized dynamically considering the uncertainties and the options created into the project basic design.

Modeling the Option to Expand, step-by-step:

1. Define the quantity of wells “deep-in-the-money” to start the basic investment in development;
2. Define the maximum number of optional wells;
3. Define the timing (or the accumulated production) that the reservoir information will be revealed;
4. Define the scenarios (or distributions) of marginal production of each optional well as function of time.
   Consider the depletion if we wait after learn about reservoir;
5. Add market uncertainty (modeling as a stochastic process as the model of reversion + jumps for oil prices);
6. Combine uncertainties using Monte Carlo simulation (risk-neutral simulation if possible, next FAQ);
7. Use optimization method to consider the earlier exercise of the option to drill the wells, and calculate option value.

Monte Carlo for American options is a frontier research area. See the page on Monte Carlo for Real Options.

Petrobras-PUC are starting a research project using Monte Carlo for real options (American type). The idea is to select the best mutually exclusive alternative under uncertainty to develop an oilfield.