Real Options with Monte Carlo Simulation

This new website section focuses real option models using Monte Carlo simulations, a very flexible way to model and to combine the uncertainties.

The Monte Carlo method solves a problem by simulating directly the physical process, and is not necessary to write down the differential equations that describe the behavior of the system. This is very general and is valid not only for our real options problem as in other areas of knowledge like physics, chemistry, etc. In our case, the Monte Carlo simulation permits simulate several sources of uncertainties that affect the value of our real option, given an optimal rule of exercise.

For several state variable (several sources of uncertainties), real options models suffer the problem of the curse of dimensionality, which limit the model solution with others methods. For example, for more than three or four state variables, both lattice and finite-difference methods face several difficulties and are not practical.
However, for simpler real options models, Monte Carlo is not the better solution because is very time-consuming in terms of computation. So, the interest on Monte Carlo simulation approach is related to solve complex real options models.

Most real options models are American-type options (earlier exercise feature) so that the Monte Carlo simulation must be used together with some optimization method in order to get the threshold curve (earlier exercise free-boundary).

This section includes the topics (many topics are placed in other pages):

Bibliography on Monte Carlo Simulation:
1) Monte Carlo for American Options;
2) Quasi-Monte Carlo (Low Discrepancy Sequences) Methods; and
3) Books, Classics and Miscellaneous in Monte Carlo Methods

Monte Carlo for European Real Options with Animation

Research Report: Real Options with Monte Carlo + Optimization with Genetic Algorithms

Quasi-Monte Carlo Simulation (practical use of low-discrepancy sequences).

Monte Carlo and Quasi-Monte Carlo Internet Links.

Monte Carlo Simulation of Stochastic Processes. Updated!

Short History of Monte Carlo Simulation

The name "Monte Carlo" appeared in the World War II times, and sometimes is attributed to the researcher Nicholas Metropolis, inspired in the interest of Stanislaw Ulam, his colleague of Manhattan Project at Los Alamos, in the poker game. Monte Carlo, the capital of Monaco, was a known reference for gambling.
According Eckhardt, Ulam invented the Monte Carlo method in 1946 while pondering the probabilities of winning a card game of solitaire (see the Ulam description on this event). However, Metropolis "attributes the germ of this statistical method to Enrico Fermi, who had used such ideas some 15 years earlier" see the webpage on Metropolis.
According Liu (2001, p.vii-viii): "The basic idea underlying the method was first brought up by Ulam and deliberated between him and von Neumann in a car when they drove together from Los Alamos to Lamy. Allegedly, Nick Metropolis coined the name 'Monte Carlo', which played an essential role in popularizing the method". Liu comments that the Los Alamos scientists aiming to take advante of the first "super" computer MANIAC, invented a statistical sampling-based technique to solve problems related to stochastic neutron diffusion in atomic bomb project and for estimating eigenvalues of the Schrödinger equation.
Winston (1996, p.22) wrote that the term was coined by mathematicians S. Ulam and J. von Neumann in the feasibility project of atomic bomb by simulations of nuclear fission, and they given the code name Monte Carlo for these simulations.

The first Monte Carlo paper, "The Monte Carlo Method" by Metropolis & Ulam, was published in 1949 in the Journal of the American Statistical Association.
Since then, several different areas has been using the Monte Carlo simulations. With the advent of personal computers and the popularization of faster computational machines, the Monte Carlo simulations has been increasing popular as an important alternative for the solution of complex problems.

The main interest in real options applications are for American type options applications, so I set one special bibliographical topic for this.
The use of more advanced techniques of sampling, improving simulation speed and accuracy, is the second topic of our bibliography.
There is a last topic, which comprises more general references, like text-books, on this fascinating topic.

1) Monte Carlo for American Options

2) Quasi-Monte Carlo (Low Discrepancy Sequences) Methods

3) Books, Classics and Miscellaneous in Monte Carlo Methods

Acworth, P. & M. Broadie & P. Glasserman (1996): "A Comparison of Some Monte Carlo and Quasi-Monte Carlo Techniques for Option Pricing"
in Niederreiter et al. (Eds.), Monte Carlo and Quasi-Monte Carlo Methods 1996 - Springer-Verlag New York, Lectures Notes in Statistics, 1998, pp.1-18

Andersen, L. (2000): "A Simple Approach to the Pricing of Bermudan Swaptions in the Multifactor Libor Market Model"
Journal of Computational Finance, Winter 1999/2000, vol.3, n^o 2, pp.5-32

Andersen, L. & M. Broadie (2004): "Prial-Dual Simulation Algorithm for Pricing Multidimensional American Options"
Management Science, vol.50, n^o 9, September 2004, pp.1222-1234

Averbukh, V.Z. (1997): "Pricing American Options Using Monte Carlo Simulation"
Doctoral Dissertation, Cornell University, August 1997, 53 pp.

Barraquand, J. & D. Martineau (1995): "Numerical Valuation of High Dimensional Multivariate American Securities"
Journal of Financial and Quantitative Analysis, vol.30, n^o 3, pp.383-405

Barraquand, J. & T. Pudet (1994): "Pricing of American Path Dependent Contingent Claims"
Digital/PRL Research Report n^o 37, January 1994, 44 pp.

Boyle, P. & M. Broadie & P. Glasserman (1997): "Monte Carlo Methods for Security Pricing"
Journal of Economic Dynamics and Control, June 1997, vol.21, n^o 8-9, pp.1267-1321

Boyle, P.P. & A.W. Kolkiewicz & K.S. Tan (2002): "Pricing American Derivatives Using Simulation: A Biased Low Approach"
in Fang, K.-T. & F.J. Hickernell & H. Niederreiter, Eds., Monte Carlo and Quasi-Monte Carlo Methods 2000 - Springer-Verlag Berlin Heidelberg, 2002, pp.181-200

Broadie, M. & P. Glasserman (1997): "Pricing American-Style Securities Using Simulation"
Journal of Economic Dynamics and Control, June 1997, vol.21, n^o 8-9, pp.1323-1352
See an online calculator with the method of this paper, using Java applet at Meier & Haug's American Monte Carlo calculator webpage.

Broadie, M. & P. Glasserman & G. Jain (1997): "Enhanced Monte Carlo Estimates for American Option Prices"
Journal of Derivatives, vol.5, pp.25-44

Carr, P. & G. Yang (1998): "Simulating American Bond Options in an HJM Framework"
Working Paper, Morgan Stanley & Open Link Financial, February 1998, 22 pp.

Carriere, J.F. (1996): "Valuation of the Early-Exercise Price for Options Using Simulations and Nonparametric Regression"
Insurance: Mathematics and Economics, vol.19, 1996, pgs.19-30

Castillo-Ramírez, A. (2000): "An Application of Natural Resource Evaluation Using a Simulation-Dynamic Programming Approach"
Journal of Computational Finance, Winter 1999/2000, vol.3, n^o 2, pp.91-107

Castro, A.L. (2000): "Avaliação de Investimento de Capital em Projetos de Geração Termoelétrica no Setor Elétrico Brasileiro Usando Teoria das Opções Reais" (Evaluation of Capital Investment in Thermoelectric Generation Projects in the Brazilian Electricity Sector Using Real Options Theory)
M.Sc. Dissertation, Dept. of Industrial Engineering, PUC-Rio, April 2000, 106 pp. (in Portuguese)

Charnes, J.M. (2000): "Using Simulation for Option Pricing"
Proceedings of the 2000 Winter Simulation Conference, 2000, 7 pp.

Cortazar, G. (2000): "Simulation and Numerical Methods in Real Options Valuation"
Working Paper, PUC de Chile, 2000, 24 pp.

Cortazar, G. & E.S. Schwartz (1998): "Monte Carlo Evaluation Model of an Undeveloped Oil Field"
Journal of Energy Finance & Development, vol.3, n^o 1, pp.73-84; and also Working Paper UCLA #1-98, PUC-Chile and UCLA, January 1998, 20 pp.

Dias, M.A.G. (2002): "Investment in Information in Petroleum: Real Options and Revelation"
Working Paper, Dept. of Industrial Engineering, PUC-Rio, April 2002, 38 pp.

Dias, M.A.G. (2001): "Selection of Alternatives of Investment in Information for Oilfield Development Using Evolutionary Real Options Approach"
Working Paper, Dept. of Electrical Engineering, PUC-Rio, January 2001, 29 pp., presented at the 5th Annual International Conference on Real Options, UCLA, Los Angeles, July 2001

Dias, M.A.G. (2000): "Real Options Evaluation: Optimization under Uncertainty with Genetic Algorithms and Monte Carlo Simulation"
Working Paper, Dept. of Electrical Engineering, PUC-Rio, July 2000, 23 pp.

Douady, R. (2000): "Bermudan Option Pricing with Monte-Carlo Methods"
in Marco Avellaneda, Eds., Quantitative Analysis in Financial Markets - Volume III, World Scientific Publishing Co., 2001, pp.314-328

Fu, M.C. & S.B. Laprise & D.B. Madan & Y. Su & R. Wu (2000/1): "Pricing American Options: A Comparison of Monte Carlo Simulation Approaches"
Working Paper, University of Maryland at College Park, April 2000, 44 pp., and Journal of Computational Finance, Vol.4, n^o 3, Spring 2001, pp.39-88

Gamba, A. (2002): "Real Options Valuation: a Monte Carlo Simulation Approach"
Working Paper 2002/03, Faculty of Management, University of Calgary, 2002, 40 pp.

Garcia, D. (2000): "A Monte Carlo Method for Pricing American Options"
Working Paper, University of California at Berkeley, January 2000, 43 pp.

Grant, D. & G. Vora & D.E. Weeks (1996): "Path-Dependent Options: Extending the Monte Carlo Simulation Approach"
Management Science, vol.43, n^o 11, November 1997, pp.1589-1602

Grant, D. & G. Vora & D.E. Weeks (1996): "Simulation and Early-Exercise of Option Problem"
Journal of Financial Engineering, vol.5, n^o 3, September 1996, pp.211-227

Ibáñez, A. (2004): "Valuation by Simulation of Contingent Claims with Multiple Early Exercises Opportunities"
Mathematical Finance, vol.14, n.2, April 2004, pp.223-248

Ibáñez, A. & F. Zapatero (1999): "Monte Carlo Valuation of American Options Through Computation of the Optimal Exercise Frontier"
Working Paper, Instituto Tecnológico Autónomo de México & University of South California, August 1999, 30 pp.

Longstaff, F.A. & E.S. Schwartz (1998/2001): "Valuing American Options By Simulation: A Simple Least-Square Approach"
Review of Financial Studies, vol.14, n^o 1, Spring 2001, pp.113-147, and Working Paper n^o 25-98, UCLA, November 1998, 38 pp.

Moreno, M. & J.F. Navas (2001): "On the Robustness of Least-Squares Monte Carlo (LSM) for Pricing American Derivatives"
Working Paper, Universitat Pompeu Fabra and Instituto de Empresa (Spain), April 2001, 36 pp.

Picazo, J.A. (2002): "American Option Pricing: A Classification-Monte Carlo (CMC) Approach"
in Fang, K.-T. & F.J. Hickernell & H. Niederreiter, Eds., Monte Carlo and Quasi-Monte Carlo Methods 2000 - Springer-Verlag Berlin Heidelberg, 2002, pp.422-433

Pizzi, C. & P. Pellizzari (2002): "Monte Carlo Pricing of American Options - Using Nonparametric Regression"
Working Paper, University of Venice, Italy, August 2002, 15 pp.

Raymar, S.B. & M.J. Zwecher (1997): "Monte Carlo Estimation of American Call Option on the Maximum of Several Assets"
Journal of Derivatives, Fall 1997, vol.5, pp.7-24

Rebonato, R. & I.A. Cooper (1996/7): "Coupling Backward Induction with Monte Carlo Simulations: A Fast Fourier Transform (FFT) Approach"
Revision of July 1997 and IFA Working Paper n^o 236-1996, London Business School, August 1996, 26 pp.

Rogers, L.C.G. (2001/2): "Monte Carlo Valuation of American Options"
Mathematical Finance, vol.12, n^o 3, July 2002, pp.271-286, and Working Paper, University of Bath (UK), 2001, 19 pp.

Tilley, J. (1993): "Valuing American options in a Path Simulation Model"
in Dupire’s Eds., Monte Carlo, Risk Books, 1998 – Reprinted version of the original published in Transaction of the Society of Actuaries, vol.45, 1993, pp.83-104

Tseng, C.-L. & G. Barz (1998): "Short-Term Generation Asset Valuation"
PSerc Working Paper n^o 98-20, October 1998, 10 pp.

Tsitsiklis, J.N. & B. Van Roy (2001): "Regression Methods for Pricing Complex American-Style Options"
IEEE Transactions on Neural Networks, Vol. 12, No. 4, July 2001, pp. 694-703

Tsitsiklis, J.N. & B. Van Roy (1999): "Optimal Stopping of Markov Processes: Hilbert Space Theory, Approximation Algorithms, and an Application to Pricing High-Dimensional Financial Derivatives"
IEEE Transactions on Automatic Control, vol. 44, no 10, October 1999, pp. 1840-1851

Whiteside, M.W. & C. Drown & G. Levy (2001): "General Solution for Option Analysis and Valuation Using a Branching Monte Carlo Method"
SPE paper no 71412, presented at the 2001 SPE Annual Technical Conference and Exhibition held in New Orleans, Louisiana, 30 September-3 October 2001, 10 pp.

Winston, W.L. (1999): "Decision Making Under Uncertainty – with RiskOptimizer"
Palisade Co., Eds., 1999, 244 pp.

Wu, R. & M.C. Fu (2000): "Optimal Exercise Policies and Simulation-Based Valuation for American-Asian Options"
Working Paper, University of Maryland at College Park, April 2000, 30 pp.

Barret, J.W. & G. Moore & P. Wilmott (1992): "Inelegant Efficiency"
Risk, vol.5, n^o 9, 1992, pp.82-84

Berman, L. (1996): "Comparison of Path Generation Methods for Monte Carlo Valuation of Single Underlying Derivative Securities"
Working Paper RC20570, IBM Research Division, October 1996, 13 pp.

Birge, J.R. (1995): "Quasi-Monte Carlo Approaches to Option Pricing"
Technical Report 94-19, DIOE, University of Michigan, revision of June 1995, 28 pp.

Brotherton-Ratcliffe, R. (1994): "Monte Carlo Motoring"
Risk, vol.7 n^o 12, December 1994, pp.53-57

Caflisch, R.E. & W. Morokoff & A. Owen (1997): "Valuation of Mortgage-Backed Securities Using Brownian Bridges to Reduce Effective Dimension"
in Dupire's Eds., Monte Carlo, Risk Books, 1998, pp.301-314 - Reprinted version of the original published in Journal of Computational Finance, vol.1, 1997

Fang, K.-T. & F.J. Hickernell & H. Niederreiter, Eds. (2002): "Monte Carlo and Quasi-Monte Carlo Methods 2000"
Springer-Verlag Berlin Heidelberg, 2002, 548 pp.

Fang, K.-T. & Y. Wang (1994): "Number-Theoretic Methods in Statistics"
Chapman & Hall, UK, 1994, 340 pp.

Fox, B.F. (1999): "Strategies for Quasi-Monte Carlo"
Kluwer Academic Publishers, 1999, 368 pp.

Galanti, S. & A. Jung (1997): "Low-Discrepancy Sequences: Monte Carlo Simulation of Option Prices"
Journal of Derivatives, Fall 1997, pp.63-83

Gentle, J.E. (1998): "Random Number Generation and Monte Carlo Methods"
Springer- Verlag New York, Inc., 1998, 247 pp.

Hellekalek, P. & G. Larcher, Eds. (1998): "Random and Quasi-Random Point Sets"
Springer-Verlag New York, 1998, 332 pp.

Joy, C. & P.P. Boyle & K.S. Tan (1996): "Quasi-Monte Carlo Methods in Numerical Finance"
Management Science, vol.42, n^o 6, June 1996, pgs.926-938

Jung, A. (1998): "Improving the Performance of Low-Discrepancy Sequences"
Journal of Derivatives, Winter 1998, pp.85-95

L'Ecuyer, P. & C. Lemieux (2001): "Recent Advances in Randomized Quasi-Monte Carlo Methods"
Survey Report, Université de Montréal & University of Calgary, 2001, 55 pp.

Li, J.X. (2000): "Quasi-Monte Carlo Algorithm for Pricing Options"
Revista de Análisis Económico, vol.15, n^o 1, June 2000, pp.111-119

Moro, B. (1995): "The Full Monte"
Risk, vol.8, n^o 2, February 1995

Morokoff, W.J. (1998): "Generating Quasi-Random Paths for Stochastic Processes"
SIAM Review, vol.40, n^o 4, December 1998, pp. 765-788

Morokoff, W.J. (1997): "Generating Quasi-Random Paths for Stochastic Processes"
Working Paper, UCLA, Mathematics Dept., February 1997, 28 pp.

Morokoff, W.J. & R.E. Caflisch (1994): "Quasi-Random Sequences and Their Discrepancies"
SIAM Journal of Scientific Computing, vol.15, n.6, November 1994, pp.1251-1279

Niederreiter, H. (1992): "Random Number Generation and Quasi-Monte Carlo Methods"
SIAM, CBMS 63, 1992, 241 pp.

Niederreiter, H. & P. Hellekalek & G. Larcher & P. Zinterhof, Eds. (1998): "Monte Carlo and Quasi-Monte Carlo Methods 1996"
Springer-Verlag New York, Lectures Notes in Statistics, 1998, 448 pp.

Niederreiter, H. & P.J.-S. Shiue, Eds. (1994): "Monte Carlo and Quasi-Monte Carlo Methods in Scientific Computing - Proceedings of a Conference in Las Vegas, 1994"
Springer-Verlag New York, Lectures Notes in Statistics 106, 1995, 372 pp.

Niederreiter, H. & J. Spanier, Eds. (2000): "Monte Carlo and Quasi-Monte Carlo Methods 1998"
Springer-Verlag Berlin Heidelberg New York, Proceedings Claremont Conference 1998, 470 pp.

Ökten, G. (1999): "Applications of a Hybrid-Monte Carlo Sequence to Option Pricing"
in Niederreiter & Spanier (Eds.), Monte Carlo and Quasi-Monte Carlo Methods 1998 - Springer-Verlag, 2000, pp. 391-406

Owen, A.B. (2000): "Monte Carlo Extension of Quasi-Monte Carlo"
Working Paper, Stanford University, 7 pp.

Owen, A.B. (1998): "Monte Carlo, Quasi-Monte Carlo and Randomized Quasi-Monte Carlo"
in Niederreiter & Spanier (Eds.) Monte Carlo and Quasi-Monte Carlo Methods 1998, Springer-Verlag, 2000, Proceedings Claremont Conference 1998, pp.86-97

Papageorgiou, A. (1999): "Fast Convergence of Quasi-Monte Carlo for a Class of Isotropic Integrals"
Working Paper, Columbia University, Dept. of Computer Science, June 1999, 11 pp.

Paskov, S.H. (1997): "New Methodologies for Valuing Derivatives"
in Dempster & Pliska, Eds., Mathematics of Derivatives Securities, Cambridge University Press, 1997, pp.545-582

Paskov, S. & J. Traub (1995): "Faster Valuation of Financial Derivatives"
Journal of Portfolio Management, Fall 1995, pp.113-120

Press, W.H. & S.A. Teukolsky & W.H. Vetterling & B.P. Flannery (1992): "Numerical Recipes in C"
Cambridge University Press, Second Edition, 1992, 994 pp.

Snyder, W.C. (2000): "Accuracy Estimation for Quasi-Monte Carlo Simulations"
Mathematics and Computers in Simulation, vol.54, 2000, pp.131-143

Tan, K.S. & P.P. Boyle (2000): "Applications of Randomized Low Discrepancy Sequences to the Valuation of Complex Securities"
Journal of Economic Dynamics & Control, vol.24, pp.1747-1782

Tezuka, S. (1998): "Financial Applications of Monte Carlo and Quasi-Monte Carlo Methods"
in Random and Quasi-Random Point Sets, P. Hellekalek & G. Larcher, Eds., Springer-Verlag New York, 1998, pp.303-332

Willard, G.A. (1997): "Calculating Prices and Sensitivities for Path-Independent Derivative Securities in Multifactor Models"
Journal of Derivatives, Fall 1997, pp.45-61

Asmussen, S. & P. Glynn & J. Pitman (1995): "Efficient Monte Carlo Simulation of Security Prices"
Annals of Applied Probability, vol.5, n^o 4, 1995, pp. 875-896

Banks, J., Eds. (1998): "Handbook of Simulation - Principles, Methodology, Advances, Applications, and Practice"
John Wiley & Sons, 1998, 849 pp.

Banks, J. & J.S. Carson II & B.L. Nelson & D.M. Nicol (2001): "Discrete-Event System Simulation"
Prentice-Hall, Inc., 3rd Ed., 2001, 594 pp.

Bouchard, B. & N. Touzi (2004): "Discrete-Time Approximation and Monte-Carlo Simulation of Backward Stochastic Differential Equations"
Stochastic Processes and their Applications, vol.111, 2004, pp.175-206

Bouleau, N. & D. Lépingle (1994): "Numerical Methods for Stochastic Processes"
John Wiley & Sons, Inc., 1994, 359 pp.

Boyle, P. (1977): "Options: A Monte Carlo Approach"
Journal of Financial Economics, May 1977, pp.323-338

Bratley, P. & B.L. Fox & L.E. Schrage (1987): "A Guide to Simulation"
Springer-Verlag New York Inc., 2nd Ed., 1987, 397 pp.

Clewlow, L. & A. Carverhill (1994): "On the Simulation of Contingent Claims"
Journal of Derivatives, Winter 1994, pp.66-74

Clewlow, L. & C. Strickland (1998): "Implementing Derivatives Models"
John Wiley & Sons Ltd., 1998, 309 pp.

Doucet, A. & N. de Freitas & N. Gordon, Eds., (2001): "Sequential Monte Carlo Methods in Practice"
Springer Verlag New York, 2001, 581 pp.

Duan, J.-C. & J.G. Simonato (1995): "Empirical Martingale Simulation for Asset Prices"
CIRANO Working Paper n^o 95s-43, October 1995, 17 pp.

Duffie, D. & P. Glynn (1995): "Efficient Monte Carlo Simulation of Security Prices"
Annals of Applied Probability, vol.5, n^o 4, 1995, pp.897-905

Dupire, B., Eds. (1998): "Monte Carlo – Methodologies and Applications for Pricing and Risk Management"
Risk Books, 1998, 348 pp.

Dupire, B. & A. Savine (1998): "Dimension Reduction and Other Ways of Speeding Monte Carlo Simulation"
in Dupire (Eds.), Monte Carlo - Methodologies and Applications for Pricing and Risk Management, Risk Books, 1998, pp.51-63

Evans, M. & T. Swartz (2000): "Approximating Integrals via Monte Carlo and Deterministic Methods"
Oxford University Press, New York, 2000, 288 pp.

Fishman, G. S. (2001): "Discrete-Event Simulation - Modeling, Programming and Analysis"
Springer-Verlag New York Inc., 2001, 537 pp.

Fishman, G. S. (1996): "Monte Carlo – Concepts, Algorithms and Applications"
Springer-Verlag New York Inc., 1996, 698 pp.

Flatto, J.P. & L.L. Gardner (2000): "Using Information Generated by a Discrete Event Simulation to Evaluate Real Options in a Research and Development Environment"
Proceedings of the 2000 Winter Simulation Conference, 2000, pgs.2040-2047

Freitas Filho, P.J. de (2001): "Introdução à Modelagem e Simulação de Sistemas - com Aplicações em Arena" (Introduction to Modeling and Simulation of Systems - with Applications in Arena) Visual Books Ltda, 2001, 322 pp. (in Portuguese)

Galli, A. & M. Armstrong & B. Jehl (1999): "Comparing Three Methods for Evaluating Oil Projects: Option Pricing, Decision Trees, and Monte Carlo Simulations"
SPE paper n^o 52949, presented at the 1999 SPE Hydrocarbon Economics and Evaluation Symposium, Dallas, 20-23 March 1999, Proceedings pp. 91-99; Shorter version appeared in Journal of Petroleum Technology, October 1999, pp.44-49

Gentle, J.E. (1998): "Random Number Generation and Monte Carlo Methods"
Springer- Verlag New York, Inc., 1998, 247 pp.

Glasserman, P. (2004): "Monte Carlo Methods in Financial Engineering"
Springer-Verlag New York, Inc., 2004, 596 pp.

Herzog, T.N. & G. Lord (2002): "Applications of Monte Carlo Methods to Finance and Insurance"
ACTEX Publications, Inc., Winsted (USA), 2002, 264 pp.

Iman, R.L. & W.J. Conover (1982): "A Distribution-Free Approach to Inducing Rank Correlation Among Input Variables"
Communications in Statistics, Part B - Simulation and Computation, vol.11(3), 1982, pp. 311-334

Jäckel, P. (2002): "Monte Carlo Methods in Finance"
John Wiley & Sons Ltd, 2002, 222 pp.

Janicki, A. & A. Weron (1994): "Simulation and Chaotic Behavior of a-Stable Stochastic Processes"
Marcel Dekker, Inc., Pure and Applied Mathematics Series, 1994, 355 pp.

Kalos, M.H. & P.A. Whitlock (1986): "Monte Carlo Methods"
John Wiley & Sons, Inc., 1986 (reprinted by Wiley-VCH Verlag, 2004), 186 pp.

Knuth, D.E. (1998): "The Art of Computer Programming - Vol.2: Seminumerical Algorithms"
Addison-Wesley, 3rd Ed., 1998, 762 pp.

Law, A.M. & W.D. Kelton (1991): "Simulation Modeling & Analysis"
McGraw-Hill, Inc., 2^nd Edition, 1991, 759 pp.

Lawler, G.F. & L.N. Coyle (1999): "Lectures on Contemporary Probability"
American Mathematical Society, 1999, 99 pp.

Lee, S-H & P.W. Glynn (1999): "Computing the Distribution Function of a Conditional Expectation via Monte Carlo: Discrete Conditioning Spaces"
Proceedings of the 1999 Winter Simulation Conference, pp. 1654-1663

Liu, J.S. (2001): "Monte Carlo Strategies in Scientific Computing"
Springer Verlag New York, 2001, 343 pp.

Madras, N. (2002): "Lectures on Monte Carlo Methods"
American Mathematical Society, 2002, 103 pp.

Manno, I. (1999): "Introduction to the Monte Carlo Method"
Akadémiai Kiadó, Budapest, 1999, 162 pp.

McCullough, B.D. & B. Wilson (2001): "On the Accuracy of Statistical Procedures in Microsoft Excel 2000"
Working Paper, Drexel University and Pace University, July 2001, 10 pp.

McKay, M.D. & R.J. Beckman (1979): "A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code"
Technometrics, vol.21, n⁰ 2, May 1979, pp.239-245
OBS: The classic paper on Latin Hypercubic Sampling.

Metropolis, N. & S. Ulam (1949): "The Monte Carlo Method"
Journal of the American Statistical Association, vol.44, n⁰ 247, September 1949, pp.335-341

Morgan, B.J.T. (1984): "Elements of Simulation"
Chapman & Hall/CRC, 1984, 351 pp.

Murtha, J.A. (1993/5): "Decisions Involving Uncertainty – An @Risk Tutorial for the Petroleum Industry"
James A. Murtha (Publisher), 1993 (second printing 1995), 171 pp.

Nelson, B.L. (1995): "Stochastic Modeling – Analysis & Simulation"
McGraw-Hill, Inc., 1995, 321 pp.

Ripley, B.D. (1987): "Stochastic Simulation"
John Wiley & Sons, Inc., 1987, 237 pp.

Robert, C.P. & G. Casella (1999): "Monte Carlo Statistical Methods"
Springer-Verlag New York, Inc., 1999, 507 pp.

Ross, Sheldon M. (1997): "Simulation"
Academic Press, 2^nd Edition, 1997, 283 pp.

Rubinstein, R.Y. (1981): "Simulation and the Monte Carlo Method"
John Wiley & Sons, Inc., 1981, 278 pp.

Rubinstein, R.Y. & B. Melamed (1998): "Modern Simulation and Modeling"
John Wiley & Sons, Wiley Series in Probability and Statistics, 1998, 352 pp.

Severance, F.L. (2001): "System Modeling and Simulation - An Introduction"
John Wiley & Sons, Ltd., 2001, 506 pp.

Sobol, I.M. (1994): "A Primer for the Monte Carlo Method"
CRC Press LLC, 1994 (from the 4th ed. in Russian, 1985), 107 pp.

Stein, M. (1987): "Large Sample Properties of Simulations Using Latin Hypercubic Sampling"
Technometrics, vol.29(2), May 1987, pp.143-151

Tavella, D. (2002): "Quantitative Methods in Derivatives Pricing - An Introduction to Computational Finance"
John Wiley & Sons, Inc., 2002, 285 pp.

Traub, J.F. & A.G Werschultz (1998): "Complexity and Information"
Cambridge University Press, 1998, 139 pp.

Usábel, M.A. (1998): "Applications to Risk Theory of a Monte Carlo Multiple Integration Method"
Insurance: Mathematics and Economics, vol.23, 1998, pgs.71-83

Vose, D. (2000): "Risk Analysis - A Quantitative Guide"
John Wiley & Sons, 2nd Edition, 2000, 418 pp.

Winston, W.L. (1998): "Financial Models Using Simulation and Optimization"
Palisade Co., Eds., 1998, 500 pp.

Zwillinger, D. & S. Kokoska (2000): "Standard Probability and Statistics Tables and Formulae"
Chapman & Hall/CRC, 2000, 554 pp.

Monte Carlo for European Real Options with Animation

There are some real options applications which can be modeled as European type options. The main example is for single stage R&D projects (which is not possible to exercise earlier, the research and tests need to be complete before some the development phase) and for markets with strong first-mover advantages (in the sense of Lieberman & Montgomery, 1988), so that typically the product development option will be exercise immediately after the R&D ending (conditional to a positive NPV for the development). In this case, the waiting value is zero for the development phase and the R&D can be modeled as European option with time to expiration equal to the estimate time to complete the R&D project.
If the R&D expected cost is lower than its European option value, the R&D project is valuable and shall be started.

For European real options case, sometimes is possible to use the Black-Scholes solution (without dividends, because there is no opportunity cost to retain the option). In this case only one underlying market uncertainty is relevant.
In others case is better to consider other underlying uncertainties, like costs, preferences, demand, price, etc. For more complex cases of several sources of uncertainties (but remaining European), the Monte Carlo simulation is a good alternative.

Let us see one simple example, with only one source of uncertainty (market uncertainty), using a risk-neutral simulation. The case is divided into two sequential animations and described below.

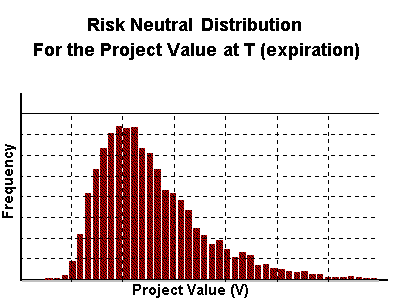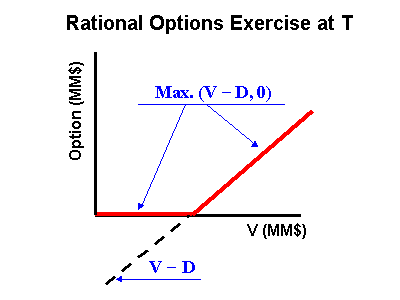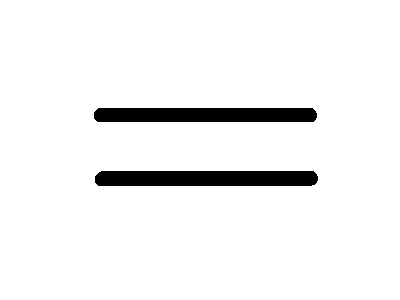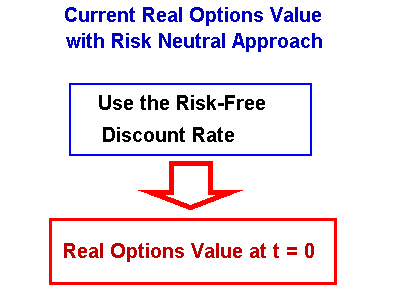
The first and second steps are to simulate the risk-neutral sample paths for the underlying asset (project value or output price) and to take the cross-section distribution at the expiration T. You get the risk neutral distribution for the underlying asset.
The figure below illustrates these initial steps:

For details on the risk-neutral simulation, including the difference of a real simulation, see the FAQ 4.

With the risk-neutral distribution of the project value V at the expiration (T), the next step is to apply the options thinking. Rational managers will exercise the option only if this exercise results in positive expected values:
F (T)= max. (NPV, 0). In other words, managers are not obligated to exercise negative NPV projects. This equation creates an asymmetry in the distribution of the real option value F(T). This asymmetric risk-neutral distribution for the European-type real options at T displaces the expected value to the higher value and represents the active management of real options.
The current value (t = 0) of the real options in this case is just to take the present value using the risk-free discount rate. The figure below shows this process.

In short, the European type (real) option valuation with Monte Carlo simulation is performed with the steps:

1. Simulate risk-neutral sample paths for the underlying asset (project value or output price);
2. Take the cross-section distribution at the expiration T, getting risk neutral distribution for the underlying asset;
3. Apply the options thinking F (T)= max. (NPV, 0);
4. Calculate the expected value of the option value at the expiration;
5. Use the risk-free discount rate and calculate the present value of the option value.

For more realistic cases, other stochastic process can be easily added into the Monte Carlo framework, for example for the development cost, and also technical uncertainties that will be revealed along the R&D project.

This paper started in my doctoral discipline "Applied Evolutionary Computation" that I performed in the first semester of 2000, in the Electrical Department of PUC-Rio.
Evolutionary approach like genetic algorithms, is a very flexible technique that has been used lately in several applications of engineering and few but growing applications in finance.

The main idea is: the genetic algorithm (GA) evolves the earlier exercise free-boundary (threshold curve) of the American option and a risk-neutral Monte Carlo simulation is used to evaluated the GA guess.
In the GA terminology, each guess is an organism (or chromosome) and the most adapted organisms (that is, with higher option value evaluated by the Monte Carlo simulation) has more probability to disseminate their genetic material, throughout the new generations. The genes are characteristics of the proposed solution, and here are or points in the threshold curve and/or parameters of a multipiece function threshold curve.

This approach is more general in the sense that, in a near future, it can get good solutions (near the optimal) for any free-boundary problem, not only in financial-economics.

The main drawback of this procedure is the necessity to run a simulation for every new threshold generated by the GA algorithm, so that to get a near optimal threshold demand a lot of time.

However, for the user point of view, the evolution of a solution (like the GA approach) is a very flexible method for Monte Carlo with American options because is a direct maximization method. So that with the passage of time, the faster computation environment this method will become very promising.
The alternative is the famous Bellman dynamic-programming, which typically performed backwards. The problem of to joint the forward-looking Monte Carlo with a backward optimization, delayed the use of Monte Carlo method for American options until the 90's.
Nowadays, there are a lot of research in this area (see bibliography), but not for using a modern direct maximization method like evolutionary computing. This research aims to fill this lacuna.

The potential of this method is its flexibility for the user modeling, reducing the problem of "curse of modeling", permitting a large popularization of real options modeling for people without a comprehensive finance knowledge.
The only commercial tool available combining Monte Carlo simulation and optimization with genetic algorithms is the Excel add-in RiskOptimizer, from Palaside. This tool has advantages like its great flexibility, but also important limitations (user cannot choose the fraction of the population to be replaced in the steady-state reproduction among others).
These issues are discussed in the paper below.

Complex real options models for project economics evaluation suffer the curse of dimensionality, with several sources of uncertainties and with several options to invest in information. Details from the changing practical reality highlight the curse of modeling problem. Monte Carlo simulation is considered a good way to face these problems, but there is the difficult problem to optimize.
This paper presents a model of optimization under uncertainty with genetic algorithms and Monte Carlo simulation. This approach permits to get new insights for the real options theory.
Using the Excel-based software RiskOptimizer for a simple case (with a known value) and for a more complex real options model with investment in information. Some results from several experiments are presented with improvement suggestions. The strengths and weaknesses of RiskOptimizer are pointed out.

Download the compressed (zip) Word for Windows 97 file with the complete paper:

genetic_alg-real_options-marco_dias.zip, with 816 KB.