FAQ Number 6

Is True that Mean-Reversion Always Reduces the Option Premium?
What Is the Effect of Jumps over the Option Premium?

Answers: no and let us see the jump effect.

• First, we'll see some different process to model the uncertainty over the oil prices (for example);
• Second, we'll compare the option premium for an oilfield using different stochastic processes
• All cases are at-the-money real options (current NPV = 0);
• The equilibrium price is 20 $/bbl for all mean-reversion cases.

Geometric Brownian Motion (GBM)

This is the most popular stochastic process, underlying the famous Black-Scholes-Merton options equation.

• GBM: expected curve is a exponential growth (or decrease);
• Prices have a log-normal distribution in every future time; and
• The variance of dP grows linearly with the time.

Mean-Reverting Process

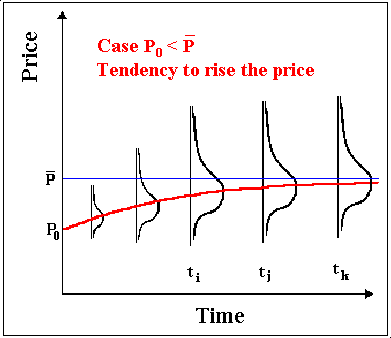
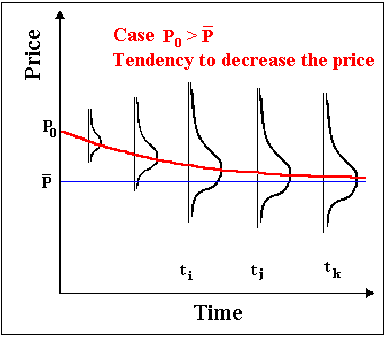
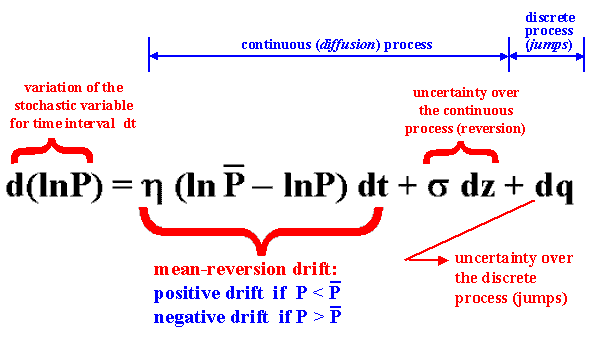
In this process, the price tends to revert toward a long-run average price (or an equilibrium level) P.

• Model analogy: spring (reversion force is proportional to the distance between current position and the equilibrium level);
• In this case, variance initially grows and stabilize afterwards;
• Charts: the variance of distributions stabilizes after t_i

Jumps

The picture below shows jumps (up and down) in the oil prices history (Brent and Similar Oils, 1970-1999).

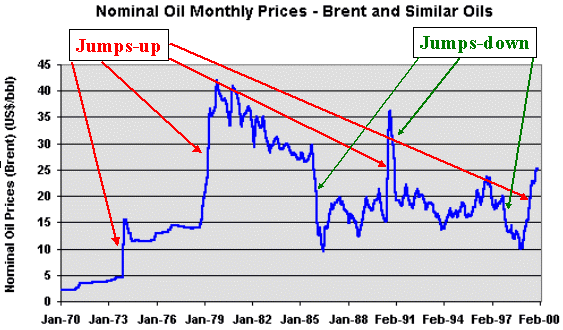
We see oil prices jumps in both directions, depending of the kind of abnormal news: jumps-up in 1973/4, 1978/9, 1990, 1999; and jumps-down in 1986, 1991, 1997.

Mean-Reversion + Jumps for Oil Prices

Was adopted in the Marlim Project Finance (equity modeling) offshore Brazil a mean-reverting process with jumps:

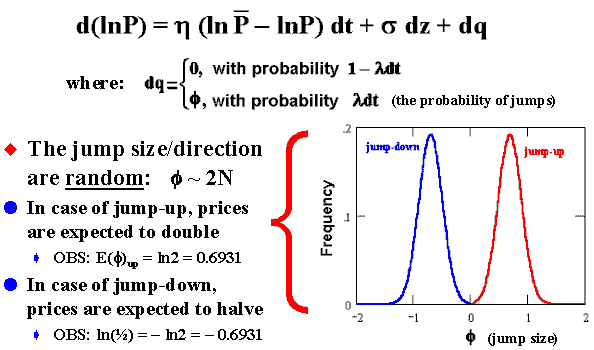
The interpretation of the jump-reversion equation is:

See more in the webpage on stochastic processes.
Now the risk premium comparison between these stochastic processes (for the definition of risk premium, see FAQ 1).

Mean-Reversion x GBM: Option Premium Comparison

The chart below compares mean-reversion (red line) with GBM (blue line) for an at-the-money project at current 25 $/bbl. The option (F) expires in three years (black line is the max. (NPV, 0) at expiration).
NPV is expected to revert from zero to a negative value (because the long run mean is assumed 20 $/bbl, and in this case the project has a negative NPV):

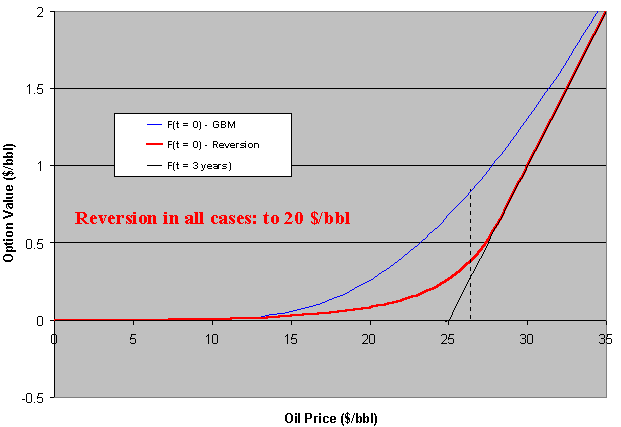
The option value (F) here is normalized by the number of barrels of the undeveloped oil reserve (so is per barrel). In order to get the undeveloped field option value, just multiply F by the reserve size.

In the case above the GBM premium is always above the mean-reverting one. But this is not general. We'll see that if the reversion is toward a positive NPV, the option premium can be higher than GBM one. But first let us see the same case above with jumps.

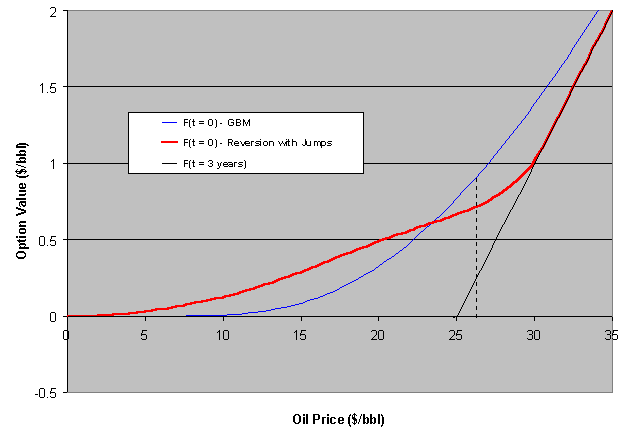
The jumps added to the reversion process increase the option premium even being neutral jumps (jumps up and down so that the mean jump is zero). Now there is a region that the reversion + jump premium is higher than GBM one.

The chart below compares the mean-reversion (without jumps) with GBM for an at-the-money project at current 15 $/bbl (suppose).
In this case the project NPV is expected to revert from zero to a positive value.

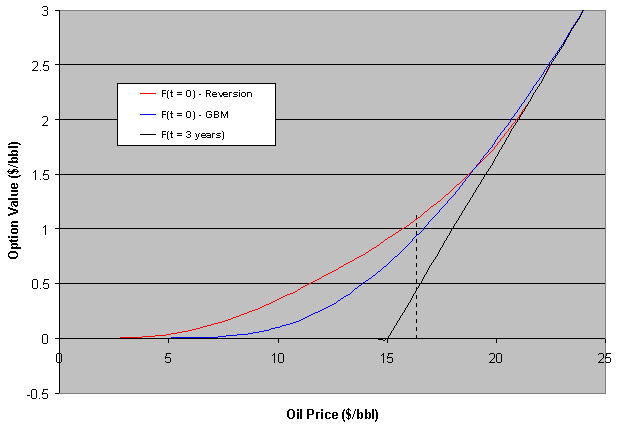
In this case the mean-reversion premium is higher than GBM one for an important region in the chart. For high oil prices, there is an inversion because the reverting drift is weak or even negative (the reversion is toward 20$/bbl in all these examples).

In this case, what happen if is added jumps into the mean-reversion process? Again, even for neutral jumps (jumps with zero mean) the risk-premium rises:

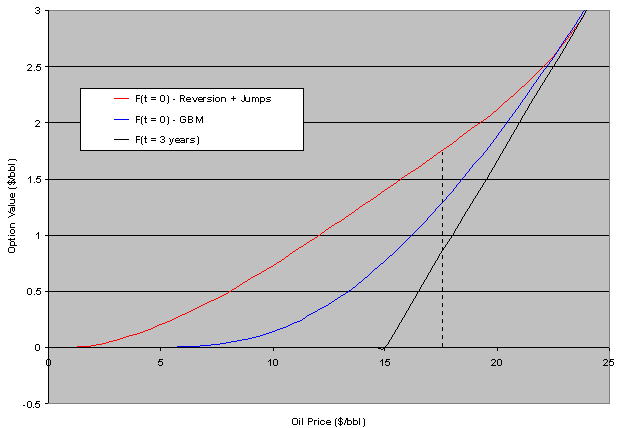
In these examples, when adding jumps, the volatility of the GBM was increased in order to compare GBM x reversion+jumps with rough equivalent volatilities.