![]() 3)
Two and Three Factors Models
3)
Two and Three Factors Models
![]() 4)
Mean-Reversion with Jumps Models
4)
Mean-Reversion with Jumps Models
![]() 5) Monte Carlo Simulation of Stochastic Processes
5) Monte Carlo Simulation of Stochastic Processes
![]() Appendixes:
Appendixes:
OBS: Because I use in this webpage the tag "Font Symbol"
for the "Greek" letters, it is recommendable to use the browser
Internet Explorer or Netscape until version 4.x. Unfortunately, Netscape
versions 6.x and 7.x don't support "Font Symbol" for the "Greeks"
letters anymore (I think this is a big drawback for the new versions of
Netscape - a negative evolution).
If you is looking the letter "s"
as "s" or "?" instead of the Greek letter "sigma",
your browser doesn't support "Font Symbol".
![]()
This popular model is the most used stochastic process in financial
economics theory and in the practice.
Geometric Brownian Motion (GBM) is an useful model by a practical point of
view. In several cases this is not the better model, even being a
reasonable mapping of probabilities with the time.
For a project value V or the value of the developed reserve that follows a Geometric Brownian Motion, the stochastic equation for its variation with the time t is:
dV = a V dt + s V dz
Where dz = Wiener increment = e dt1/2 (where e is the standard normal distribution); a is the drift; and s is the volatility of V.
In the above equation the first term of the right side is the expectation (trend) term and the second term is the variation term (deviation from the tendency or term of uncertainty).
Note that this specification from Wiener process leads to a "jumpy"
changes in the stochastic variable V.
The reason is: for a small time interval Dt,
the standard deviation movement will be much larger than the mean of stock
movement. Why? For small Dt, (Dt)
½ is much larger than Dt, and
this will determine the behavior of sample paths of a Wiener process.
For similar reasons, a Wiener process has no time derivative in a
conventional sense:
Dz/Dt =
e(Dt)-
½, becomes infinite as Dt
approaches zero.
In real options problems, there is a dividend like income stream
d for the holder of the asset. This dividend
yield is related to the cash flows generated by the assets in place. For
commodities prices this is called convenience yield or rate of return of
shortfall.
In all cases, the equilibrium requires that the total expected return
m to be the sum of expected capital gain plus
the expected dividend, so that:
m = a + d
So, the stochastic equation can be written:
dV = (m - d) V dt + s V dz
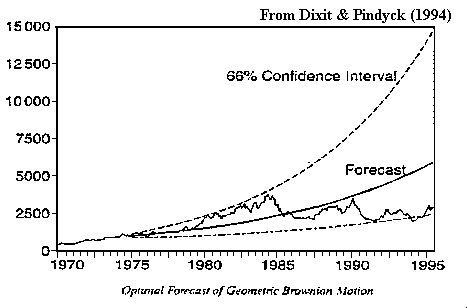
The following picture illustrates this stochastic process, showing a sample path, the 66% confidence interval, and the forecasted expected value (exponential trend line).
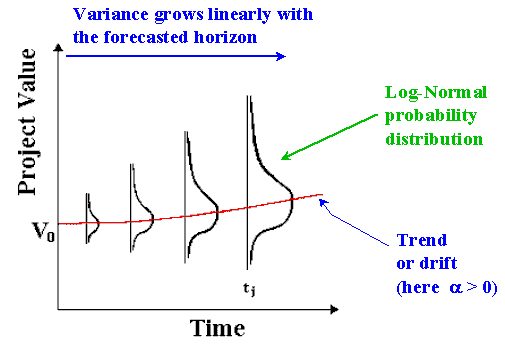
The Geometric Brownian Motion is a log-normal diffusion process, with the variance growing proportionally to the time interval. The picture below illustrate this:
Popular models like the Paddock & Siegel & Smith model, uses
this stochastic process.
By using the American call option analogy, several software written in
financial options can be used for real options.
This model is explained in The Classic
Model webpage. The deduction of
the option equation with contingent claims method, is also available
there.
Geometric Brownian Motion (GBM) has the great advantage of the
simplicity.
Metcalf & Hasset (1995) important paper comparing GBM with
mean-reversion by the point of view of cumulative investment,
conclude that even mean reverting being a more plausible assumption
(allowing for supply responses to increasing prices), cumulative
investment is unaffected by the use of mean reversion rather than GBM.
This is a defense against more sophisticated models. However, sometimes
more precise models are required, mainly for competitive business, where
even a not large difference is important .
Somebody can ask about the utility of arithmetic rather geometric
Brownian process for real options applications. The point is that
sometimes is useful to work with arithmetic Brownian for the logarithm
of the project value.
Following Dixit's textbook The Art of Smooth Pasting (p.7):
if dV/V = a dt + s
dz, letting v = ln(V), and using Itô's Lemma we find that v
follows the arithmetic (or ordinary) Brownian motion:
dv = d(lnV) = (a - ½
s2) dt + s
dz
so,
dv = a' dt + s dz
The logarithm of V = v follows an Arithmetic Brownian Motion with drift a' and volatility s.
Although the volatility term is the same of the geometric Brownian for
V, as highlighted by Dixit, d(lnV) is different of dV/V due the
drift. In reality, by the Jensen's inequality, d(lnV) < dV/V (Itô's
effect).
There is a frequent confusion between d(lnV) and dV/V (people saying that
is the same thing). Sometimes this confusion has no practical importance
because the drift value doesn't matter for several applications (the case
of many options calculations, like the Black & Scholes famous
equation). Otherwise the drift matters, as in the case of the
first hitting time that a stochastic
value cross a free boundary, because it do depend of the drift. The drifts
of d(lnV) and dV/V are different.
Due its simplicity can be interesting to work with the logarithm
diffusion equation, so using arithmetic Brownian motion, easing
probabilistic calculus such as the confidence interval or even easing
Monte Carlo simulations.
Suppose you want to use the historical prices data of the biotech company shares, in order to estimate the uncertainty (stochastic process) of a new project in this area. It's possible to estimate the parameters to use in real options as the underlying variable uncertainty.
Using the logarithm of V format, you can estimate ( a - ½ s2 ) as the average values of lnVt - lnVt - 1.
With the same historical series you can get an estimation of the
volatility s by taking the standard
deviation of lnVt - lnVt
- 1. This value permits also to
estimate the drift.
The stochastic process of V, geometric Brownian motion (GBM), means that
this variable follows a lognormal process over time with the following
parameters.
The expected value of V at the instant t is (starting t0 = 0):
E[Vt] = V0 exp( at )
The standard deviation (SDV) of a lognormal distribution with the expected value E[Vt] is:
SDV[Vt] = V0 exp( a t ) [ exp( s2 t ) - 1] ½
Note that the standard deviation of the return is not equal the
volatility (people common confusion).
Defining return: Rt = (Vt/Vt
- 1) - 1, we
get:
SDV[Rt] = exp( a t ) [ exp( s2 t ) - 1] ½
However, in most cases to work with normal distributions of the
logarithm of V is easier than with the lognormal distribution itself.
The ln(Vt) is normally distributed with mean
E[ln(Vt)] = ln(V0) + ( a - ½ s2) t
The standard deviation associated with the expected value ln(Vt) is:
SDV[ln(Vt)] = s t ½
For a normal distribution, a confidence interval of 95% is
approximately equal to the mean +/- 2 standard
deviations. So, is easy to construct 95% confidence interval for the
logarithm of V.
For confidence interval of lognormal distributions, is easy to calculate
with spreadsheets like Excel, which has the function: loginv(probability,
mean from ln(x), standard deviation of ln(x)); for confidence interval
(CI) of 95%, set "probability" in the loginv function as 0.025
(for lower bound of the 95%CI) and 0.975 (for upper bound of the 95%CI).
As noted by Campbell & Lo & MacKinlay (The Econometrics of Financial Markets, Princeton University Press, 1997, p.363), in the empirical job, is possible to joint annual data with monthly data. The ease of using irregularly sampled data is one of the greatest advantages of continuous-time stochastic processes, by the econometric point of view.
Campbell & Lo & MacKinlay (p.364) point the practical question: "how
to sample returns so as to obtain the best estimator?"
The answer depends if the parameter to be estimate is the drift
a or if is the volatility s.
For the drift, the best (estimator with lower variance) is the
estimator based on as long a time span as possible. The number of
samples is not important as the time between observations.
However, for the volatility, the best estimator is based on as
many observations as possible, regardless of what their sampling
interval is.
In short, a large number of observations is important only for
volatility, whereas samples of a long time interval is important only for
the drift.
For several applications, people is interested only in the volatility
estimative, whereas for other applications (forecasting, first hitting
time, simulations of the real process, estimative of risk-premium, etc.)
the drift is important.
For mean-reversion process, we will see that the drift parameters are
important even for complete markets.
To simulate Vt following a Geometric Brownian Motion, the best alternative is using the the logarithm transformation ln(Vt), which follows an Arithmetic Brownian Motion, being normally distributed. In this way is valid to use a large Dt. The equation is:
ln(Vt) = ln(V0) + ( a - ½ s2) t + s t ½ e
Where e is a standard normal
distribution (normal with mean equal to zero and unitary variance). So,
the simulation procedure is to get values of ln(Vt) for each
sampled value of e.
Using a large number of samples, the resulting average value simulated for
ln(Vt) is expected to be near of the analytical value
presented before and so the standard deviation of a normal distribution.
With this simulation, is easy to present a chart with transformed values for Vt instead ln(Vt).
The more general case is to simulate the paths of V(t), from t = 0 to t = T. In this case, given the value of V at time t, we get the value of V at time t+1 using:
Vt+1 = Vt Exp[ ( a - ½ s2) Dt + s Dt ½ e]
Where Exp[.] is the exponential operator.
Real versus Risk-Neutral Simulations:
In the equations above we are simulating real stochastic
processes, not risk-neutralized stochastic processes.
The simulations of real processes can be necessary in some applications.
For instance in risk management, specially simulations for purpose of Value
at Risk estimative, which we must use the real process (not the
risk-neutral) to estimate the (real) losses possibilities in a given
horizon. In real options and other applications, the estimative of the
true expected first hitting time using simulation, must use
simulation of the real process.
There are other applications which is better to simulate risk neutral sample paths and/ or the risk neutral distributions at any time t.
In derivatives valuation, assuming complete markets, is necessary
to use risk neutral simulation. Using real simulation and discounting with
the (underlying asset) risk-adjusted discount rate, give the right result
for the present value of the underlying asset but the wrong
result for the derivative. The point is that the risks of the derivative
and underlying asset are different (so risk-adjusted discount rate are
different).
As curiosity, in general, for vanilla call the derivative discount rate is
higher than the underlying asset one whereas for vanilla put the discount
rate is lower (can be even negative). The risk-adjusted discount rate for
derivatives has not interest because to estimate is necessary to solve the
contingent claims valuation, and after the solution is not necessary to
know the discount rate.
For risk-neutral simulation, we can calculate value from future
simulated values, using the risk free discount rate.
Risk neutral simulation presents a modified drift, r -
d instead the real drift a. This is
equivalent to subtract a risk premium from the drift (see Trigeorgis'
textbook, 1996, p.102):
Where l is the underlying asset market premium of risk in the sense that m = a + d = r + ls, (m = risk-adjusted discount rate for the underlying asset).
The figure below presents the equations of both real and risk-neutral simulations for the case of GBM:

Two sample paths from real simulations and risk neutral simulations are showed in the example below (for geometric Brownian). Note that the paths are parallel, and the risk neutral one is a risk premium lower than real sample path.
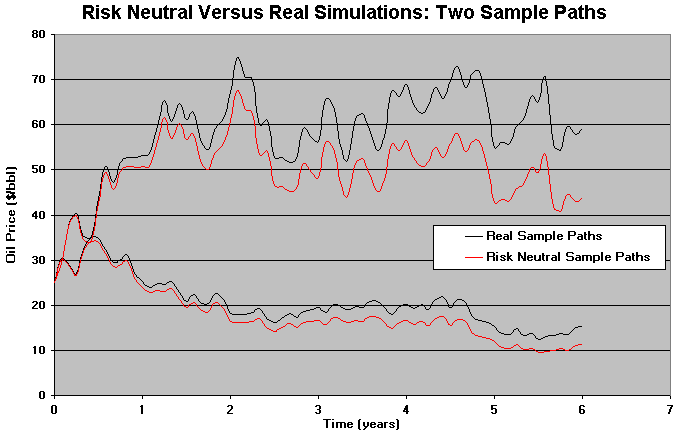
Use risk-neutral simulation for derivatives together with the risk-neutral discount rate, but remember that risk-neutral simulation is not a panacea, so that in some cases the real simulation can be more appropriate.
For risk neutral simulations and a good introduction to Monte Carlo simulation for derivatives, see Clewlow and Strickland (1998), Implementing Derivatives Models, John Wiley & Sons.
For additional details, see also the webpage on Monte Carlo Simulation of Stochastic Processes
![]()
![]()