Half-Life in Mean Reversion Processes

The original concept of half-life probably comes from the physics: measuring the rate of decay of a particular substance, half-life is the time taken by a given amount of the substance to decay to half its mass.

Let define half-life (H) of a variable x as the time for the expected value of x(t) to reach the intermediate (middle) price between the current value x(0) and the long run mean m, which the mean reverting process is converging in the long run.

Half-life gives the slowness of a mean-reversion process. So, it is an alternative parameter to the reversion speed h and there is a direct relation between H and h. This relation is showed below.

Suppose that the variable x, the logarithm of the petroleum prices P follows an arithmetic mean-reverting process also known as Arithmetic Ornstein-Uhlenbeck:

dx = h (m - x) dt + s dz . . . . . . . . (1)

Where m is the long-run mean price (or the long-run equilibrium level which the logarithm of the prices tends to revert); h is the speed of reversion; and the other terms have the usual meaning presented before in the page of stochastic processes.

E[dx] = h (m - x) dt . . . . . . . . (2)

This logarithm of oil prices half-life is deducted below. From eq.2 we have the deterministic equation:

dx / (m - x) = h dt

Integrating from x₀ (t₀) to the expected price at the instant t₁, denoted by x₁( t₁), and letting Dt = t₁ - t₀, we get:

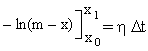
Hence:

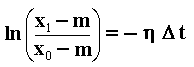. . . . . . . . (3)

For Dt = half-life H, by definition we have that (x₁ - m) = 0.5 (x₀ - m). Substituting:

ln(0.5) = - h H

- ln(2) = - h H

The half-life is finally given by the equation:

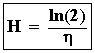. . . . . . . . (4)

I thank to Ping Wu from McMaster University to point out an error in an older version of this page, which I used other variation of mean-reverting process as example (the error was due a typo in a very known book of formulas and mathematical tables).

Why not? Half-Life For Discount Factors

One interesting extension of this concept is related with the discounting factor used for present calculations purposes.

A known "rule of thumb" is that the present value of a future cash flow drops to the half for 10 years using a 7% discount rate or for 7 years using a 10% discount rate ("rule 7-10"). These figures are approximate.
In these case we can say, alternatively, that the half-life for a 7% discount rate is 10 years; or the half-life of a 10% discount rate is 7 years.

So, for every discount rate we can associate an half-life for that.
Conclusion: instead a rate of discount we can express the discounting effect alternatively by the discounting half-life concept, which gives the number of years to decay half of value.

This alternative view of the discounting effect can be useful for project thinking with future flexibilities, to take an idea of discounted value.
The point of view of discount rate instead discounting half-life, is better in others cases where a notion of rentability is important instead the notion of future cash flow value.

So, in real options applications the alternative of discounting half-life concept can be more useful than the discount rate itself. Large half-life values means low discount rates and vice versa, with the numbers give a notion of present value of future benefits.