Using Real Options in Project Evaluation
Contribution by Jerry Flatto from North Carolina A&T University
This article was written for Resource - The Magazine for Life Insurance Management Resource is published by th Life Office Management Association (LOMA) which is the education arm of the insurance industry.
Introduction
One of the primary responsibilities of management is the allocation of available resources in their organization. Unfortunately, there are never enough available resources to go around to perform all the tasks and projects desired. Therefore, management has to decide which projects will be pursued.To evaluate competing projects, the majority of organizations use some form of quantitative analysis technique. Among the common techniques used are net present value, internal rate of return, and payback.
This article will discuss the concept of "real options" which can be used to expand your existing analysis methods. I will discuss why many of the existing analysis techniques underestimate the value of a project and how real options can capture some of the benefits that slip through the cracks under existing analysis methods.
Traditional Analysis Methods
The majority of organizations use some sort of quantitative analysis methods to capture the estimated costs and benefits associated with a proposed project. The most popular methods include internal rate of return, net present value, and payback.However, these methods have some associated assumptions that can result in the value of an investment being underestimated. They assume management's passive commitment to a certain "operating strategy" (e.g., to initiate the project immediately, and operate it continuously at a set scale until the end of its pre-specified expected useful life). The methods also ignore the synergistic effects that an investment project can create. Sometimes the performance of one project will allow you to perform a second project that would not have been possible without the first (e.g., many research and development projects). Therefore, the analysis usually underestimates investment opportunities because it ignores management's flexibility to alter decisions as new information becomes available.
One way to compare the results of a traditional analysis with an analysis that includes management's flexibility is to look at distributions of the potential outcomes. In the analysis process, a number of the input variables can vary depending on different assumptions such as best case, worst case, etc. You can run the analysis a number of times varying the possible inputs. You can then plot the results of the analysis. The x-axis is the range of possible outcomes, usually in dollars. The y-axis is the probability of any particular outcome.
If you perform this type of analysis using the traditional tools such as net present value, you end up with a figure similar to Figure 1. The most likely value will have the highest probability and the other outcomes will have lower probabilities associated with them and you end up with a standard "bell" curve. The "most likely" value is in the center, "worst case" analyses are to the left of center, and "best cases" are to the right of center.
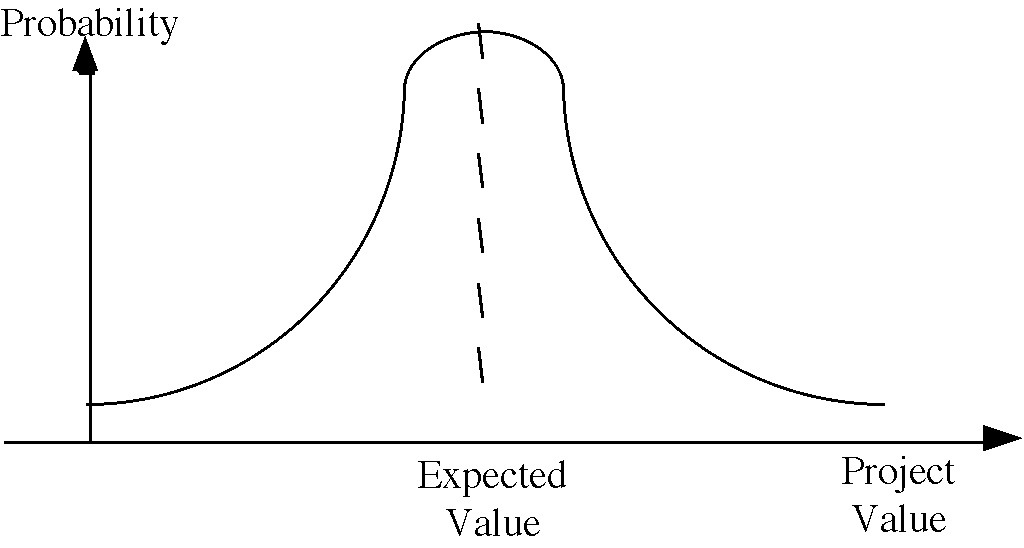
Figure 1: Project value, excluding the flexibiity value
In reality, even though the analysis methods have the inherent assumptions I discuss above, your actions are not limited by these assumptions. You have the flexibility to alter decisions as further information becomes available. If future conditions are favorable, you may expand the project to take advantage of these conditions. On the other hand, if the future is unfavorable, you may curtail or even cancel the project as the conditions warrant. Another way to talk about the flexibility is that it allows you to improve a project's upside potential while limiting the impact of the project's downside losses. This results in a project with a higher expected value and causes the distribution to be skewed to the right as shown in Figure 2.
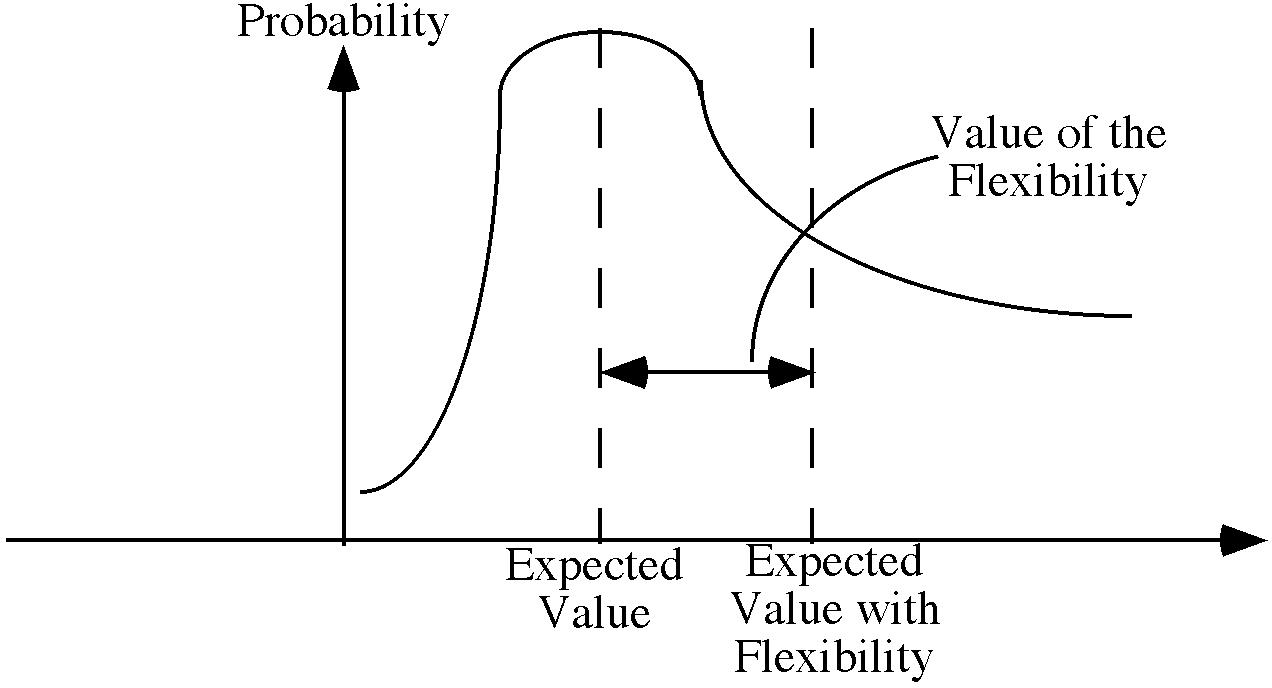
Figure 2: Project value, including the value of the flexibility
The difference between the expected value with and without flexibility is the value that the flexibility provides. One way to look at the value of the flexibility is through the use of real options.
Flexibility and Options
When we look at the flexibility associated with a project, there are a couple of types. The first type is flexibility internal to the project itself. This is the flexibility to modify the project as future conditions change. These changes can include expansion, alteration and even abandonment of the project. For example, assume you are looking to buy a new car. The only real requirement of the vehicle is that it gets you to work and back. With this is mind, you can buy any small two seat economy car to meet your needs. However, being the forward thinker that you are, you decide to buy a van with removable seats. Now, not only can you get to work, you can perform tasks not originally envisioned, like moving your mother-in-law to her new apartment that is much farther away from your house. Thus your flexibility allowed you to use your vehicle for other tasks than originally considered.The other type of flexibility is external flexibility. Performing this project will now allow you to perform another project that may not have been possible originally. For example, your long lost uncle leaves you enough money to buy a cabin near your favorite ski area. Without this cabin, your were limited in the times you go skiing since it was not possible to get reservations at the resort hotels on a short term notice. Purchasing the cabin gives you the flexibility to go skiing whenever you want. You are no longer at the mercy of the hotels.
As these two examples show, flexibility is a valuable commodity and usually the more flexibility associated with a project the better. The concept of real options is an extension of the concept of flexibility. When people talk about flexibility, they are typically describing it in qualitative and subjective terms. A van has more flexibility in allowing you to move items than a two seat compact car. Having to stay at a resort hotel is less flexible than having your own cabin.
Thus one problem when trying to measure the value of the flexibility is the difficulty in trying to get two or more people to agree on the value of the flexibility. Consider that to a person who loves skiing, the cabin provides great flexibility. Another person, whose idea of winter sports is walking from the heated car to the shopping mall, may consider that the cabin provides minimal flexibility.
Another problem associated with valuing flexibility is trying to include the value with other costs and benefits that are quantified (i.e., dollars). Studies of management decision making has shown that management typically assigns greater weight to quantitative costs and benefits than qualitative benefits (e.g., flexibility). Therefore, even though a project's flexibility may provide great benefits, these benefits are typically given less consideration when comparing a project's tangible costs and benefits.
It is for the reasons just discussed that the concept of real options was developed. What separates the concept of real options from the concept of flexibility is the method by which each are measured. Flexibility is typically measured qualitatively (e.g., a van is more flexible than a car). The goal of real options is to measure the flexibility quantitatively and generate a dollar value for the flexibility. A real options model of the decision to purchase a van instead of a two seat compact car might find the added flexibility is worth $5000.
Stock Options
Before I get into a discussion of real options, I want to talk about financial (e.g., stock) options. The development of real options is based upon option pricing theory and stock options. The majority of you may have heard of stock options while probably only a few have heard of real options.Those of you involved in either corporate or personal investment may already be familiar with stock options. A call stock option allows you to purchase stock at an agreed upon price before or on a certain date. For example, you can have a call option to purchase stock at $75 which is good for seven days. The stock is presently at $65. If the price of the stock rises above $75 within the next week, you can purchase the stock for $75, even though it may be worth $150. On the other hand, if the stock never goes above $75, your stock option is worthless and you forfeit the cost you paid for the option.
Let me give another example in case you are not familiar with stock options. When you go to get a fixed rate mortgage, you are concerned that the interest rate may rise during the time that the mortgage takes to be approved. Many mortgage companies allow you to "lock in" the existing rate for a fee. This lock is good for an agreed upon time, such as 60 days. If the mortgage rate stays constant, then you are "out" the fee with no gain. On the other hand, if rates do rise, you are protected against having to pay a higher interest rate. [In my case, if the interest rate dropped, I was still "locked-in" to the higher rate.] This is also an example of a financial option.
Five variables determine the value of the financial option. These five variables are the stock price (e.g., $65), exercise price (e.g., $75), interest rate, time to option expiration (e.g., seven days), and the volatility of the stock price. I am not going to get into any details of how a stock option is priced but it is effectively a "cookbook" operation. By that I mean that if you want to buy an option on a stock, if you know the value of the five variables above, you can look up the cost of the option in a table. In other words, it is not a long and complicated process to determine the price of a stock option.
Real Options
The major difference between a financial (e.g., stock) option and a real option is that real options are applicable to "real" assets. A real asset is usually tangible such as a factory, car, etc. while a financial asset typically consists of stocks, bonds, currency, etc.Let me give an example showing how the flexibility of a project is important in evaluating the project's benefits. You want to buy a wood stove that can supplement your home's heating system. You go and look at some different stoves. You end up comparing two stoves that are identical with the exception that one stove burns wood only (cost - $500) while the second stove can burn both wood and coal (cost - $700). Not surprisingly, the stove that burns both wood and coal is more expensive. Why would you even consider buying the wood and coal stove? Because of the added flexibility that the wood and coal burning stove provides. Is the flexibility of the wood and coal stove worth $200? It's going to depend on variables such as the relative price, availability, ease of use, etc. of wood and coal. Complicating the process is that the value for the variables will change over time. In the end, it comes down to a subjective judgement on your part whether the additional $200 cost for the wood and coal burning stove is worth it.
If you get together with a group of friends to discuss which of the two stoves to buy, you should all agree that the wood and coal stove is more flexible than the wood stove. However, I bet you won't get complete agreement on how valuable the flexibility difference is between the two stoves. On the other hand, if you develop a real options model of the decision you might find that the added flexibility of the wood and coal stove is worth $275. Since the additional cost is less than that ( i.e., $200), buying the wood and coal burning stove is worthwhile. [One obvious comment that I bet some of you are thinking right now is that a person can "cook" the numbers in the real options model to get any value desired. To be honest, that is true. But a person can "cook" the numbers in any type of analysis to get the desired results. Does this mean that you never use any quantitative analysis in your job?]
Types of Real Options
Some previous work in real options has generated a taxonomy that has broken down real options into six categories based upon the type of flexibility provided. The six categories are: the option to defer; the option for staged investments; the option to change scale; the option to abandon; the option to switch; and the option to grow.The option to defer occurs when you can put off a decision until some date in the future. This allows management to determine if resources should be spent on a project at that future date. For example, your long lost uncle leaves you a gold mine instead of cash. A trip to the mine shows you that there is gold in the mine, however, the cost of removing the gold is more than the gold is worth. If you keep the mine, you have to pay a small property tax on the land every year. Paying the small tax allows you to defer the decision on whether to extract the gold. Right now the gold is essentially worthless, but the price of gold might suddenly sky rocket making the cost of extracting the gold worthwhile. Therefore paying the small tax allows you to delay a decision on whether to extract the gold if conditions change.
The option for staged investments occurs when a project investment happens in a series of outlays that allows the project to be abandoned in mid-stream if conditions become unfavorable. The development of a project can be considered a series of options. Each stage in development can be considered an option on the value of future stages. You decide you want to convert the gold mine you inherited in the previous example to a tourist attraction. You draw up the plans for a theme park, however, you build only one concession stand at first. If people really enjoy your attraction, you can expand the concession stand and add a ride. On the other hand, if there is suddenly an overabundance of gold mine attractions, you don't have to expand your concession stand. Thus building in stages allows you to abandon or change the project if future conditions deteriorate.
The option to change scale can result in the project being expanded, contracted, or shut down and restarted. Depending on market conditions that prevail at a particular time, the rate of resource expenditure can be adjusted to meet the new conditions. For example, you have decided to replace your personal computer. You go to your local computer superstore and see what is available. Presently you are using your computer only for word processing and spreadsheets. You don't really need a high end color monitor, 32 megabytes of memory, and a 2 gigabyte hard drive. So why don't you buy a stripped down system that is adequate for your existing needs? Because you don't know what you will need to do tomorrow with your machine. You might suddenly have to develop a world wide web site for your company or put together presentations, or suddenly your kids decide they "need" to have the latest games. Even if your needs don't change, the existing software you use may be revised and you no longer have the capability to run the new versions on your machine. Thus you go with the machine that is more powerful than your existing needs so that if your needs expand, you do not have to start over and purchase a new machine. [I remember when I bought my first hard drive which stored 20 megabytes. I would never be able to fill it up. Now to install Microsoft Office on my machine requires 75 megabytes of disk space and to run it at a reasonable speed requires a processor four generations beyond what was in my first Macintosh.]
The option to abandon allows the company to abandon a project if the market conditions drop dramatically. The company can then sell off any assets available to offset the loss or switch those assets to other projects. For example, you buy a new IBM PC to be able to work at home. Suddenly your company decides to switch from PC to Macintosh and you need to get a new computer. Fortunately, your teenage daughter is going away to college in a couple of months and will be required to buy a PC. So you now turn over your PC to your daughter and no longer have to buy her one. Therefore, even though the PC cost $2,000, you didn't lose all the value when you abandoned it. Rather you shifted the resource to another location where it was still valuable.
The option to switch allows an organization to change either the input mix or output mix of a facility. If environmental conditions change, this option provides the flexibility to alter either the process (i.e., input mix) or product (i.e., output mix). The wood stove example used previously is an example of this type of option.
The option to grow is used when an initial investment is required for further development. The project can be considered a link in a chain of related projects. Each project in the link is required for the future growth. An organization may invest in research and development even though it typically has a negative value when looked at in isolation. It invests because of the future growth value of the results of that research and development. For example, you are convinced that your gold mine attraction will be a winning idea but presently the only way to reach the gold mine is by a one mile burro ride. You decide to build a road to connect your gold mine with the highway. Looking at the costs and benefits of the road in isolation, the costs outweigh the benefits and it does not make sense to put in the road. However, you realize that without the road, the rest of the project is not feasible. Therefore, you decide to build the road even with its negative cost analysis because it is required as part of the first stage in developing your gold mine attraction.
Many projects do not have only a single real option that is applicable to them. Depending on the type of project, more than one real option may need to be considered when computing the value of the real options. For example, I used the same gold mine example in three of the cases above. However it is important to realize that these real options can interact in various ways. The value of the interacting multiple options may not be equivalent to the value of the individual real options added together.
Value of the Real Options
Until now I have been describing the concept of real options and have provided some general examples of how real options are part of everyday projects. Now I want to talk about the way that it might be possible to measure the value of the real options.I previously mentioned how the value of a financial option may be determined. An analogy can be made between the variables that determine the value of a stock option and a real option. Table 1 shows a comparison between the two types of options.
| Stock Option | Real Option |
| Current value of stock | Gross present value of expected cash flows |
| Exercise price | Investment cost |
| Time to expiration | Time until opportunity disappears |
| Stock value uncertainty | Project uncertainty |
| Riskless interest rate | Riskless interest rate |
The cash flows are the amount of money that the project will bring in. As the expected cash flows increase, the real option becomes more valuable if the other variables are kept constant. For example, if the amount of gold that can be extracted from the mine can be doubled, then the gold mine becomes more valuable.
The investment cost is the amount of money that needs to be committed to provide the organization with the real option. Keeping the other variables fixed, increasing this amount will decrease the overall value of the real option. For example, if the cost to extract the gold doubles, the value of the mine decreases.
Increasing the time a project can be deferred increases the real option's value. As the deferment time increases, the uncertainty associated with future events decreases since there is more time to gather information about future conditions. If the future is unfavorable, the project is not pursued. If the future is favorable, the original project can be expanded to provide the maximum return. Additionally, the longer you can defer the project, the greater the likelihood that a favorable outcome may happen. For example, you can keep the gold mine for only one week. The price of gold is unlikely to rise enough during the week to warrant the extraction costs. On the other hand, if you can keep the gold mine for ten years, it is more likely that the price of gold may go up enough in that time to make mining the gold worthwhile.
The uncertainty associated with a project impacts the value of the real option. If two projects with identical values can be deferred the same amount of time, the riskier of the projects will have a greater potential value. A risky project usually provides the opportunity to generate high returns, but there is also a high probability of failure associated with the project. Since management has the flexibility to expand the project if it succeeds or abandon it if things do not go well, the associated riskiness is reduced. For example, if the price of gold remains relatively stable, the value of the gold in the mine stays stable. If gold prices can fluctuate wildly, it is more likely that the price of gold may drop dramatically. In that case, you take no action. On the other hand, if you are lucky, the price of gold greatly increases and you can extract the gold and make a profit.
Higher interest rates increase the value of the real options associated with a project. Normally, higher interest rates convert into higher discount rates that decrease the value of a project. However, higher discount rates also mean a decreased present value of the future capital needed to exercise the real option. This counterbalancing effect helps to sustain the option's value as interest rates rise. This real option can give growth oriented projects an advantage in the capital budgeting process. For example, since you have a ten year lease on your gold mine, you can wait a few years before you have to buy the needed equipment to extract the gold. The present value of the equipment is cheaper since the greater expense of the equipment is further out in time and thus less expensive in "today's" dollars.
What Has Been Done
Real options are relatively new and there is not a large body of knowledge. The majority of work on real options has been done in the academic community. The work could be broken down into three categories - conceptual, simplified models, and industry applications. The first two categories encompass the vast majority of the literature written on this topic.The conceptual articles provide the basis for real options. Some of the articles formalize the theory underlying real options. Other articles expand upon the theory and give examples of how the real options could be used to increase the value of projects in a number of different industries such as pharmaceuticals, natural resource extraction, consumer electronics, etc. These articles do not develop any quantitative models but rather discuss real options from a qualitative perspective.
The second category of literature is those articles that develop quantitative models that demonstrate how real options can impact a project's overall value. In many of the articles, the models developed are simple and examine only a few states of nature. For most, the numbers entered into the models are created by the author(s) of the article. A few of the articles use input data drawn from actual projects. The quantitative models developed are not detailed enough for actual use by management.
The third category of articles includes those that describe models sufficiently detailed to actually be used by industry to support decision making. A review of literature found only four articles that fell into this category. The first two articles provide a comparison between the results of real options models and the results of "traditional" financial analysis. In these two cases, the real option models are not used by management for any decision making purposes. The third article discusses insights gained from the use of real options to assist in the decision making process at Shell. The fourth article discusses the use of real options at Merck Pharmaceutical Company. Merck has integrated the use of real options into their formal financial analysis process.
The last article was particularly interesting. Merck Pharmaceutical Company actually uses real options to evaluate projects and assist management in evaluating potential projects. The article describes how real options are used to value research investments which typically are not amenable to traditional financial analysis techniques. Merck determines the values of the real options inherent in a project. Because of the nature of the pharmaceutical industry, development of new drugs takes a number of years before a return can be seen on the investment. In addition, development is a very risky business with many of the drugs never being marketed. Market conditions and cash flows so far in the future are difficult to predict. These factors tend to cause traditional financial analysis techniques to underestimate the value of a project.
Real options allow the potential profit from new drugs to be better incorporated in the financial model. Because of the nature of the industry, large pharmaceutical companies typically farm out initial research and development to either small companies or universities. The large company funds the research as a series of payments (i.e., staged investment). These payments give the company the right, but not the requirement, to make further investments based upon the results of the research. If traditional financial analysis techniques were used, many of the projects that yield a positive net worth under options analysis would not be pursued since the traditional net worth would be negative. The article indicates that real options analysis is currently used only for research and development projects, however, Merck would like to extend this type of analysis to "traditional" projects such as building new facilities or purchasing new companies.
In addition to the articles I just mentioned, I recently completed some research examining how real options might assist the insurance industry in evaluating information technology projects. I chose to look at information technology since it is at a disadvantage when comparing costs and benefits. Many of the benefits provided by information technology are particularly difficult to measure. Among the benefits that an information system can provide include: more information, faster information, more accurate information, increased customer satisfaction, etc.
As part of my research, I sent out a questionnaire to the chief information officers at LOMA member companies in the United States and Canada. The questionnaire asked about their existing and potential use of real options. Limited space allows me to summarize only a few of the major findings:
- Very few of the respondents had ever heard of the term "real option". After explaining what the term meant, the majority of respondents indicated that they do include at least some of the flexibility aspects of a project in their cost benefit analysis.
- In approximately 60% of the cases, the value of the real options inherent in a project made a difference between approval and disapproval.
- It appears that no companies are using formal models designed to value the real options. In the majority of cases, the value of the real options is being incorporated qualitatively.
- A majority of the companies (75%) accept projects even when the quantitative analysis does not support this action.
What Can You Do
In this article I have explained the concept of real options and how they can be used to supplement your existing analysis process. Unfortunately, the level of quantitative analysis for real options is nowhere as advanced as the quantitative models for financial (i.e., stock) options. Therefore, I don't expect any of you to be able to start generating dollar estimates for the values of the real options inherent in your projects.Rather what I hope happens is that you take another look at the projects you need to evaluate. Look at the projects for the options they provide. When possible, use the framework I described before to examine a project to see if it already contains flexibility embodied in the six types of real options. Alternately, see if the project design can be modified to include the different types of real options thus providing you with additional flexibility. Remember, additional flexibility is a benefit. Even though you can't quantitatively determine the value of the real options, you can qualitatively include the value of all the real options in the cost benefit analysis process.
I want to leave you with a comment by Steven Ross, Sterling Professor of Economics and Finance at Yale School of Management. Steven Ross was one of the individuals heavily involved in the development of option pricing theory and financial options. The quotes are from his keynote address at the 1994 Financial Management Association Annual Meeting. He states: "I have become convinced that it is time to revisit the usefulness of NPV [net present value] and to reconsider just how much stock we want to place in it." He further goes on to say: "For most investments, the usefulness of the NPV rule is severely limited. Š If modern finance is to have a practical and salutary impact on investment-decision making, it is now obligated to treat all major investment decisions as option pricing problems."
Back to the Contributions Page.