Real Options Mathematical Software Applications

Mathematical software applications, like Mathcad, Mathematica, Matlab, and Mapple, are good tools for real options applications, with the advantage over spreadsheets and program language, for some tasks. This kind of software has some facilities that ease the solution of real options models, such as facilities for numerical integration, solution of differential equations, solution of non-linear system of equations, etc.

Examples of mathematical software are Mathcad, Mathematica, Matlab, and Mapple

Mathcad Application: Entry-Temporary Stopping-Reactivation-Exit Model

Here is presented one Mathcad application for the hysteresis model presented in the Dixit & Pindyck book, chapter 7, the more complete and complex model, the example of the tanker, in the section 2, with entry (building), exit (scrapping), temporary stopping (mothballing), and reactivation (from the mothballing state).

See how to register software and licence fees.

The following figures show the Mathcad language for the tanker example, including the two systems of non-linear equations solution.

• Notation
• M = annual cost of maintaining a mothballed tanker, million $/year
• R = lump-sum cost of reactivating a mothballed tanker, in millions $
• EM = lump-sum cost of mothballing, in millions $
• E = exit cost or abandonment cost, in millions $.
  In the example this cost is negative, because the tanker has a positive scrap value.
• C = annual operational cost, in millions $/year
• I = average cost to building a new tanker with 85,000 dwt, in millions $
• P = annual revenue, in millions/year.
  Actually P = $7.3 million per year, but the future revenue is uncertain. P follow a geometric Brownian motion.
• r, d, and s, have the usual meaning, that is, risk-free interest rate, dividend yield, and volatility, respectively.

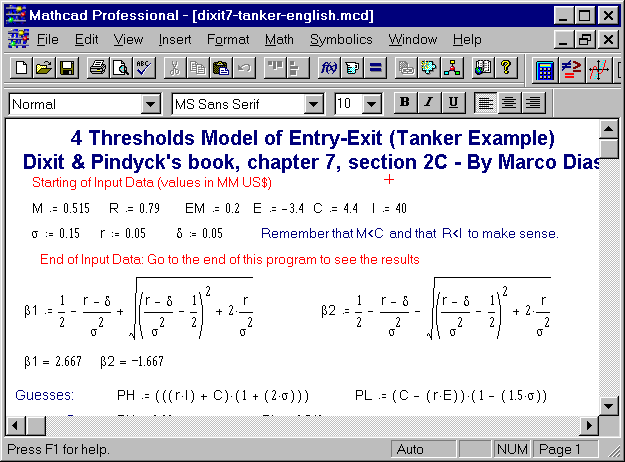
First screen shows the input data, some parameters (betas) calculation, and initial guesses for the first set of non-linear equations.

The second screen shows the first set of non-linear equations, and how get the solution for two thresholds (PM for mothballing and PR for reactivation) and for two coefficients (D1 and B3):

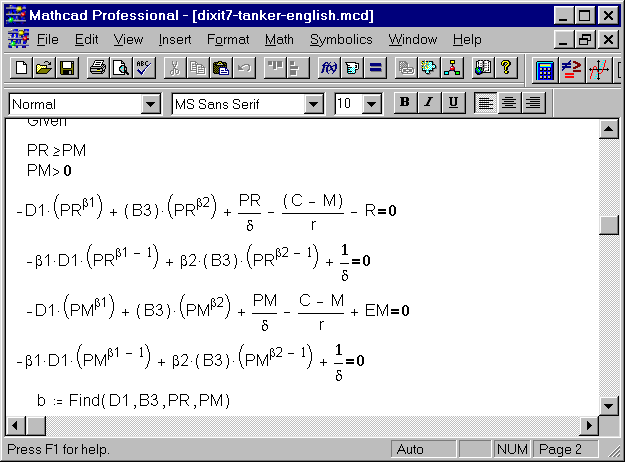
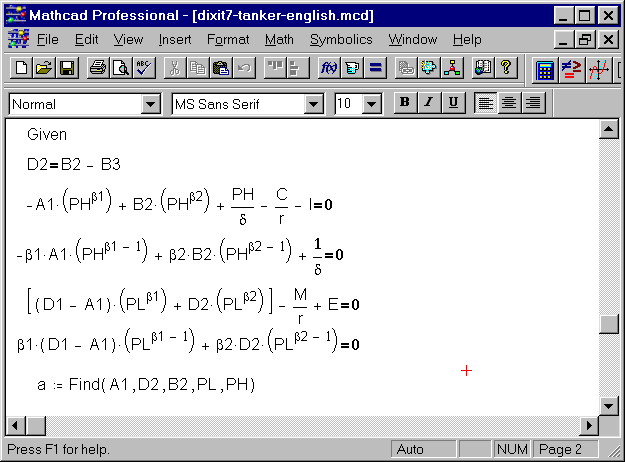
The third screen shows the second set of non-linear equations, and how get the solution for the two remained thresholds (PH for entry and PL for abandon/exit) and for three coefficients (A1, D2 and B2):

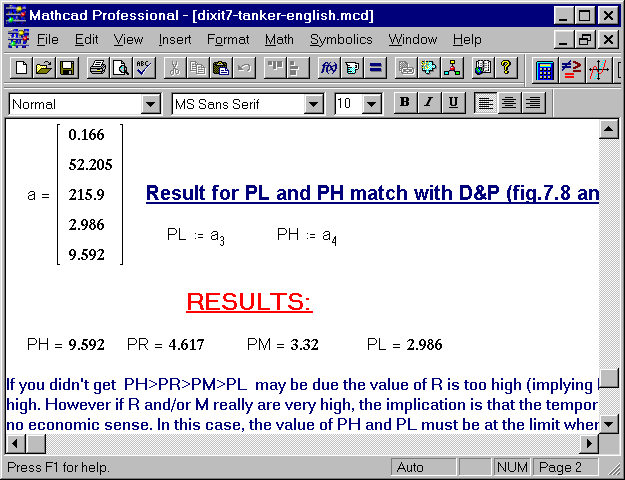
The last screen summarizes the results:

For significant different data, may be necessary to modify the initial guesses. Why? Initial guesses are important to solve sets of extremely non-linear equations (the case above).
These type of system of equations can present more than one solution.
It is possible that you find a mathematical solution but not the solution that makes sense in real options problem. If this occur, you need to find the other solution (that makes sense). In order to do this, just change the initial guesses. In the Mathcad's tanker software, look for the values between the words (key operators) "Guesses" and "Given".

In more rare cases, its possible to have problem of convergence. The stronger recommendation is again to change the initial guesses. The initial guesses that I set above, are good enough for the tanker example and in general can reproduce all the charts presented in the Dixit & Pindyck's book, without any change in the initial guesses. But in others cases could be necessary to change the initial guesses.