Real Options Selected Bibliography:
the Dixit & Pindyck Book

The "Selected Bibliography" list covers many important aspects of the options thinking. There are comments, for each book or paper, available by clicking their titles. This selection begins with the main reference, a born-classic text-book by Dixit & Pindyck: the first text-book exclusively about the real options approach to investments. This bibliographical item deserves a more detailed comments, in view of their importance to the theory.

Dixit, A.K. & R.S. Pindyck (1994): Investment under Uncertainty
Princeton University Press, Princeton, N.J., 1994 . Click here for Marco Dias' comments.

See also in the Contributions Page, An Instructor's Manual: for the Dixit & Pindyck's Investment under Uncertainty textbook by Luiz Eduardo Brandão (in Portuguese).
See also this link with the same material plus some spreadsheets.

See also in the Contributions Page, Matlab files to solve some problems from the Dixit & Pindyck's Investment under Uncertainty textbook by Luke J. Sparvero. NEW!

Back to the Bibliographical List

Back to Contents (main page)

Dixit, A.K. & R.S. Pindyck (1994): Investment under Uncertainty
The book brings an excellent theoretical and practical combination of the new approach, with their mathematics and economic foundations insights, complemented with industry typical investments decisions examples, embedded with representative industry's data.. In many times, when presenting equations, the book gives both, an intuitive/heuristic explanation and a more rigorous mathematical development.
In a rare case, a paper was written and published (outside of the books' review section) about this book (Hubbard, 1994).

The book comprises twelve chapters divided into five parts:

1. The Part I is the introduction with two chapters.
   • The Chapter 1 presents some introductory concepts (investment, the ability to wait, and so on) and and a comparison between the modern "Real Options Approach" and the neoclassical investment theory with their variants like the "Tobin's q or marginal q" and the "Jorgenson's user cost of capital". Both variants of the neoclassical model rely on the very known "net present value rule".
     This chapter presents also an overview of the book, introducing some concepts like the "hysteresis in economics", or path dependence. The chapter concludes with noneconomic applications, focusing themes like marriage, suicide, legal reform and Constitutions.
   • The Chapter 2 presents, through simple two and three period examples, the value of waiting to invest, into a value maximizing investment decision context. In the examples, the static net present value (NPV), or a NPV in "now or never" investment basis, is calculated and also a dynamic NPV (when including the flexibility to wait) calculus is performed, and the difference between the dynamic and the static is the option to wait value or the opportunity cost of investing now, rather than waiting and keeping open the option investment opportunity.
     This discrete and lattice approach was used only in this chapter (a continuous time model, with differential equation building approach, is presented in all of following chapters of the book), and with the aim to develop the reader's intuition and concepts. The several examples show the uncertainty effect in the investment decision and also others parameters effects. The financial options analogy is more closely analyzed.
     The critical price (or the threshold) is presented with the numerical examples plotted in many charts. The "bad news principle" is illustrated by examples. The chapter also introduces the "technical uncertainty" concept, when the reader begins to believe that uncertainty always leads to postpone investments: in many cases, when investment provides information, uncertainty can perform the opposite effect, stimulating the investment starting (ex: petroleum exploration and R&D investments). In this context, a negative NPV project can be optimally undertaken, because the project has an additional value that not was considered in the traditional NPV calculations: the reduction of the variance of the technical uncertainty with the accumulated investment. This value is called a shadow value because it is not a directly measurable cash flow.

2. The second part of the book is the "Mathematical Background" with more two chapters:
   • The Chapter 3 presents the stochastic process and the Itô's Lemma. Concepts such as random walk process, Markov process, Wiener process (Brownian motion), are presented in a easy way. The geometric Brownian motion with drift (a special case of the Itô process) is detailed, with equations and figures showing sample paths and optimal forecast from this process (see also the figure "Optimal Forecast of Geometric Brownian Motion" , file gif with 5988 bytes) .
     The mean-reverting process is analyzed as a more realistic economic model for some stochastic variables like the price of raw commodities such as oil or copper. The Ornstein-Uhlenbeck process equations illustrate this alternative process, and also figures showing sample paths and optimal forecast, are presented (see also the figure "Optimal Forecast of Mean-Reverting Motion" , file gif with 5924 bytes).
     The Itô Lemma is introduced as a tool, permitting the differentiation and integration of Itô process' functions.
     The reflecting barriers concept, which occurs often in economic applications (because of equilibrating mechanisms in the market), is showed with equations and research extensions are pointed out.
     Closing the chapter, the Poisson (jump) process is introduced as a way to consider the presence of infrequent but discrete jumps for the stochastic variable, or in others words, some discontinuous process in a short time interval inside of a prevailing continuous process..
   • The Chapter 4 presents the dynamic optimization under uncertainty, developing two important techniques: dynamic programming and contingent claims analysis. These tools, despite they make different assumptions about financial markets and discount rates, lead to identical results when the first one adopts the risk neutral method.
     The dynamic programing is showed for two and many periods, and also the famous Bellman's equations and the Bellman's Principle of Optimality. Optimal stopping and smooth pasting techniques are illustrated in Bellman's equations context.
     The contingent claims analysis is presented inside the dynamic replicating portfolio framework. This portfolio is built for to be risk-free, and consequently is independent of the investors' preferences: risk-averse or risk-neutral investors, with any increasing utility function, agree with the same portfolio value. The method rely on the market equilibria, where no arbitrage opportunities survives more than a very short period. The relation of this approach with the CAPM theory are pointed out, and so the insights about the quantity of the underlying assets that makes the portfolio risk-free. The smooth pasting condition and also the Poisson process are analyzed in this context. The equivalence between this approach and the dynamic programming (with the risk-neutral approach for the latter) is established.

3. The third part of the book is the "firm's decision" with three important and more practical chapters:
   • The Chapter 5 presents the decisive role of the timing in the investment opportunities decisions and valuations, where the authors points "the simple NPV rule is not just wrong; it is often very wrong". The authors shows also, even for the deterministic case, the timing flexibility adds value to investment opportunity and creates a value to waiting. The basic model is solved in both dynamic programming and contingent claims framework, illustrating their equivalence. About the validity of the contingent claims, that needs a perfectly correlated asset (spanning), the authors point out (see p.152) this market value reference is necessary not only for contingent claims, but also for CAPM: "Without spanning, there is no theory for determining the 'correct' value for the discount rate (unless we make restrictive assumptions about investors' or managers' utility functions). The CAPM, for example, would not hold, and so it could not be used to calculate a risk-adjusted discount rate in the usual way".
     The basic result for the perpetual investment opportunity can be summarized in the following equations (see p.142):

     

     
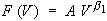
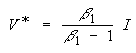
     The first equation shows the investment opportunity value (F) equal to a constant (A) times the value of implanted project (V) with a exponent which is more than one. This exponent is a function of the parameters (see p.152): risk-free interest rate (r), dividend yield (or convenience yield), and the volatility (standard deviation of the rate of variation of the project value). The second equation, points out the optimal investment rule: invest if the market value of the project is equal or more than the threshold (V*) value. The fraction multiplying the investment (I) is like a wedge which always values more than 1, and can reach values such as 2 or 3, for real parameters, and increases with the economic uncertainty.
     The characteristics of the optimal investment rule are examined, presenting four charts which show the effects of the two more important parameters (volatility and dividend yield) on both, the decision rule (V*) and the value of the investment opportunity.
     The chapter also examines alternative stochastic processes like the mean-reverting and the combined Brownian motion and Jump (Poisson) process. The authors choose the Geometric Ornstein-Uhlenbeck for the specific mean-reverting process which results, after some substitutions, in the Kummer's equation, which has a series representation (that converges) for the perpetual investment opportunity case. In the combined jump/Brownian process, also a differential equation is developed, which can be solved numerically for a more general case or, in the case of the a simplified assumption (in the event that V falls to zero, where remains forever), there is an analytical solution similar to the pure Brownian case, but adding the Poisson parameter to the risk-free rate.
     

   • The Chapter 6 examines the value of a project (V), as function of more basic variables like the output price (P). When V is a constant multiple of P, both follows the same stochastic process and with the same parameters (expected growth, volatility, dividend yield), see p.178, because the rates of variation is the same for both variables. However in general, when V is not a multiple of P, just the latter follows a geometric Brownian motion. So this chapter calculates V as function of P (this is used as boundary condition at the contact), and the investment opportunity (F) as function of P. If V follows a stochastic process and their parameters are easy to calculate, the chapter 5 approach (calculating F as a function of V) is also possible (see p.182).
     Several cases of projects characteristics are analyzed, beginning with the no operational costs case.
     In the section 2 the operational costs are considered, and are allowed temporary stopping and reactivation, in both cases without additional costs.
     The Excel spreadsheet below, available to download, illustrates the section 2 of the chapter 6. It calculates the NPV with the option to shut-down and the value of a perpetual option to invest in this project .
     Download the Excel spreadsheet dp-chapter6-nonlinear_npv.xls, with 108 KB NEW!
     Section 3 presents the variable output case, which the profit is a convex function of P (but is a concave function of the input parameter, such as labor, so the optimal choice of input maximizes the profit). V is nonlinear with P.
     The more interesting (for petroleum projects) section 4, deals with depreciation. The exponential decay case is examined for both (see p.201) without allows re-investment and allowing to invest back again after the project dies. The first case is more simple, more realistic for petroleum fields investments, and V is linear in P, allowing calculate also F as function of V, with the difference (comparing with chapter 5) that the Poisson parameter is added to dividend yield for discounting purposes. The sudden death case and a general case (exponential decay and sudden death, together) are examined, too.
     The last section examines the price and cost uncertainty case, with correlated stochastic processes. This more general case needs numerical solution, two smooth pasting conditions, and instead one threshold point, there is a line of thresholds named "free boundary". For the case analyzed (project with perpetual life and no variable output) the homogeneity of the problem allows to reduce it to one dimension case with analytical solution.
     
   • The Chapter 7 deals with entry & exit model (or hysteresis model) with some improvements in relation to early works (such as Dixit, 1989, and Brennan & Schwartz, 1985). The first case analyzed is an extreme one: if stop the production the entire capital rust and the firm must incur the whole investment again to restart it. The model considers the abandon cost, which can be positive (legal requirements like restoring the site of mine to its natural condition, and workers indemnity) or negative (alternative use for a portion of the capital or scrapping value). The differential equations are showed for the idle firm (which has the option to invest) and for the active firm (with the option to abandon), resulting in four nonlinear equations with four unknowns (two constants and the two thresholds, one to entry and other to exit), which are solved with the nice approach using the function G(P). The authors points out the spread between the two thresholds with rational expectations is farther apart than the traditional Marshallian microeconomy says (with static expectations). An example with the copper industry is presented (which is an empirical evidence of the option approach to real decisions), with many illustrating charts.
     The second section includes the temporary stopping (plants are "mothballed", and ship/tankers are laid-up), with both lump sum cost for stopping and a maintenance cost flow. So besides the investment and abandonment options, the firm has the option to stop without exit, and later to reactivate paying another sunk cost. In this case four thresholds must be calculate (entry, exit, stop, reactivate), three status are allowed to the firm, and five state changing are possible (the active firm can exit without stopping stage). Two groups of four differentials equations are presented, and numerically solved in two examples, the second one about oil tankers, and again with lots of charts.
     In the "Guide to the Literature", the authors mention a little mistake in the famous earlier Brennan & Schwartz model, which they confuse the transition between some states, using the same lower threshold notation for mothballing and for abandonment, besides the numerical example considered switches between just two states (active and mothballing, the firm never exits), because the maintenance cost was zero.

4. The fourth part of the book is the "Industry Equilibrium" with two chapters, and is more useful for economists:
   • The Chapter 8 examines the aggregated industry equilibrium under a perfect competitive environment. In opposite to the monopolist case (examined into chapters 5-7), the value of waiting for the competitive firm is zero. However, the threshold value (for entry) is the same of the previous chapters! When a price of a commodity rises and one competitive firm invests (entry), all others identical competitive firms do the same, so the price falls (because production surplus), and the threshold is an upper reflecting barrier on the price process. Firms with rational expectations will require a sufficiently high price to invest, because they know the price will fall with the competition. This high (ceiling) price coincides with the monopolist case, but for different reasons.
     In section 3 the model is extended by allowing the abandonment option, and the authors shows that the value of an idle firm is zero, for this competitive case. The copper industry example is presented in a more general situation, where is pointed the traditional microeconomic theory is out of the reality: prices above long-run average cost without attracting new entries, or prices below average variable cost without inducing exit.
     The section 4 deals only with firm-specific uncertainty (no multiplicative aggregated stochastic shock) on the demand curve. The model is settled into two stages: by paying an entry cost R (like acquiring a patent), firms earn the right to invest in production (become potential active firms), and waiting has value. Potential and active firms can die (with Poisson death probability). The entry and the investment decisions are examined, and also the distribution of firms in the industry (including the rate of new entry).
     In the last section, a general model is derived with both firm-specific and industry-wide uncertainty on the demand curve, reaching the eq.43, which is a generalization of early sections thresholds results.
     
   • The Chapter 9 presents the socioeconomic planner dilemma about policy intervention to provide additional investment incentives and also the extension of the previous chapter by relaxing the perfect competitive assumption (number of competitors is small).
     The first section examines the correspondence between social optimality and equilibrium, using the model aggregated uncertainty on demand. The value of one industry is given by the sum of the values in place of all the installed firms, and the sum of the values of options to install all the futures units. In efficient markets, dynamics and uncertainty are not reasons for policy intervention, as many times happens: a high price of goods often calls antitrust measures, and low prices often justifies trade sanctions to foreign firms. The policy of price controls is other example. Of course these governments interventions are often mistakes that can have perverse effects on market efficiency.
     In section 2, the authors examines some commonly used policies: (a) the price ceiling controls fails to achieve its intended goal of reducing the prices to consumers, the long-run effect is the opposite (see table 9.1 and figure 9.1), because the investment reduction and so the long-run supply; (b) the price floor protection induces an overproduction in declining demand industries (the long-run number of firms goes to infinity), like farmers in many countries, which stay so dependent on price supports; (c) the policy uncertainty creates by governments, as constant changes in tax policy and trade tariffs, increases the value of waiting (in detriment of investment), and/or lowers the scale of its investment, increasing the prices to consumers.
     The last section addresses the oligopolistic industry (competition is not perfect) using the stochastic game theory, which is quite recent for such applications, still more in continuous time. The fear of preemption by a rival induces early entry. The model studies the duopoly case, and calculates the value of both firms, the leader and the follower, which have two different thresholds. Even the leader needs an option premium to entry (NPV > 0 rule is still wrong). The authors indicates simultaneous investment is a mistake, because reduce the value of both firms.
     

5. The Part V, Extensions and Applications, comprises the three last chapters.
   • The Chapter 10 is very important for firms investment decisions: deals with sequential investment as analogous to compound options. The investment is staged, so completing one stage gives the right (not the obligation) to invest in the next one. The project takes time to built. The model has two state variables: the amount of capital installed (or number of stages completed) and the output price.
     The first model examines the two-stage project, which the operational profit will come only after the second stage (is not like a growth option). If the output price falls during the first stage, the firm can delays the investment in the next stage. In the second section, the model is generalized and the investment is continuous, but takes time to built (there is a maximum rate at which construction can proceed), and investment can be stopped and later restart costlessly. The table 10.1 illustrates a numerical example, with project value and the (decreasing with capital installed) thresholds. In depth analysis of many parameters from the solution are presented, including the value of construction time flexibility (the ability to speed up construction).
     The third section examines the learning curve model, which the production costs are decreasing with cumulative production, until it reaches a irreducible cost level. This is typical in aircraft industry, but also happens in others sectors, including drilling oilwells. See the figure Learning Curve and Deepwaters Wells Drilling (Offshore Brazil). File with 5327 bytes.
     This learning effect increases the value of the firm and reduces the threshold (see table 10.3).
     Section 4 examines cost uncertainty with two components: economic and technical uncertainties (together in the same variable). The technical uncertainty has value if the investment can be staged, so the learning effects (reduction of the variance of the technical uncertainty) adds value to firm and decrease the threshold required to continue the investment (see the table 10.4 for the latter). So technical uncertainty has the opposite effect of economic uncertainty.
     For details on technical uncertainty, see in the Tutorial Page the topic on Economic and technical uncertainties, and mainly the webpage on technical uncertainty.
   • The Chapter 11 examines the incremental investment and the capacity choice in a continuous time framework. The firm has a capital stock (assets in the place) but also has a project's portfolio and can grow by increasing the capital stock. The investment condition is the marketable stochastic variable (like output price) rises above the investment threshold. Projects with lower thresholds will be first candidates for investment. The choice of the capacity is performed "ex-post", not "ex-ante" (see ex-ante capacity choice) . The chapter focus is more theoretical and for economists.
     In the first section the expansion has diminishing returns of scale (the marginal revenue product is decreasing with the investment). The optimal investment policy is derived with both, dynamic Programming and contingent claims. The figure 11.1 (p.362) illustrate the incremental investment as a sequence of marginal projects. The effect of uncertainty is presented with an example using the very known Cobb-Douglas production function. Using this example, the authors show that a larger volatility (or uncertainty) means lower long-run average growth rate (less investment). The depreciation effect also is analyzed, and it acts with closed analogy for the case of a single project (the interest rate is increased by the death Poisson parameter).
     In the section two, the expansion has increasing returns of scale. This happen in situations when the firm to encounter an initial phase of increasing returns, or by geometric reasons. In this case the optimal is wait until the threshold is reached, and so make a big investment, in a large capacity (lump investment), jumping over the whole range of increasing average product.
     The third section close the chapter and presents the adjustment costs, that means the costs of changing the capital stock too rapidly. This cost are an invention of the economists, in order to explain the slowness of the investment to respond the demand shocks. The authors show the classification of these costs, including convex adjustment costs. Another look in the Tobin's q theory is presented, including these costs, and so stochastic theory insights such as the range of inaction for the investment and the barrier control that arises from irreversibility.
     An excellent complement for this chapter is the Pindyck's paper (see American Economic Review, vol.79, December 1988, pp.969-985).
   • The Chapter 12, Applications and Empirical Research is one of more interesting and practical of the book, a gold key ending.
     The section one deals with petroleum E&P investments and offshore leases valuations. I detail many aspects (including the deduction of the equations) in the Real Options in Petroleum page. The authors recommend the more important model in real options literature for petroleum investments, the Paddock, Siegel & Smith model. This model makes an analogy with financial options model (American call on continuous dividend asset). The developed reserve (producing reserves) is like an asset, the undeveloped reserve (before the investment) is like a call option, the development cost (investment) is like the exercise price, and the relinquishment is like the time to expiration. The dividend yield analogy is one of more strong aspects of the model, because is estimate using the cash flows of the project (so, is project specific). The authors also extend the model using mean-reverting stochastic process for the developed reserve value, with a discussion about the necessity or no, of this mathematically more complex process.
     The section two examines the electric utility firms dilemma due to the Clean Air Act. The firm has the following three alternatives: (a) buy pollution allowances; (b) investment for switch the fuels to the more expensive low-sulfur coal; (c) investment in a very expensive scrubbers.
     The section three analyses the timing of environmental policy. There are two kinds of irreversibility. First the pollution effect of the greenhouse gas, like global warming, has high irreversibility degree (the concentration of the gas has a natural decay rate of about one-half percent per year). Second, the environmental policy adoption is also irreversible, and implies the imposition of large sunk costs to firms and society. The problem is divided into two regions, the no-adopt policy region, and the adopt region, and two partial differential equations are derived using optimization problem (minimize the cost for the society) under uncertainty (cost has a stochastic component). Remarkably, both partial differential equations have analytical solutions!
     The last section examines the empirical issues of the investment theory. The authors show that the neoclassical investment theory has been no success in the explaining the aggregate investment behavior. Even sophisticated econometric test of Tobin's q theory, allowing delivery lags, cannot find support to their assumptions. The problem is the irreversibility was overlooked in the traditional tests. However, the econometric test of real options theory is not an easy task. First, the equations describing investment under uncertainty are non-linear. Second, can be difficult to measure the variables or parameters that reflect the key components of uncertainty. Third, the problems of aggregation: different firms have different action thresholds. However, the few econometric tests with the real options theory has been positives. The authors also show many empirical evidence of this theory, including the use by managers of high hurdles rates, in order to make only deep in the money projects.
     In short, this book is a must see, for economists, practitioners, students, sophisticated managers, and researchers.

Back to Selected Bibliography

Hubbard, R.G. (1994):

Investment under Uncertainty: Keeping One’s Option Open
Journal of Economic Literature, vol.32, December 1994, pp.1816-1831

Back to Dixit & Pindyck book's comments

Tobin's q:

This neoclassical investment model due to the Nobel Laureate J. Tobin, 1969 ("A General Equilibrium Approach to Monetary Theory", Journal of Money, Credit and Banking, 1, February 1969, pp.15-29), compares the capitalized value of the marginal investment to its purchase (replacement) cost.. The ratio is the Tobin's q. If q > 1, the firm should invest. The firm stops the investment process when their marginal investment is at such level that q = 1. If q < 1 the firm should not invest. The capitalized project value can be the observed directly if is marketable, but frequently it is computed as the expected present value of the net cash flows.

Back to Dixit & Pindyck book's comments

Jorgenson's user cost of capital:

This neoclassical investment model due to the D. Jorgenson, 1963 ("Capital Theory and Investment Behavior", American Economic Review, 53, May 1963, pp.247-259), treats the capital investment as a purchase of a durable good. The user cost of capital is defined by the rental cost of the capital, and is determined using parameters like the purchase price, opportunity cost of funds, depreciation rates, and applicable taxes. The theory compares the value of an incremental unit of capital (marginal product) and the user cost (or rental cost): the firm invests when the marginal product is greater than the user cost and stops when an equality is reached.
In this model and in the Tobin's q model, the dynamics is considered (not satisfactorily) with adaptations such as "adjustment costs" and "delivery lags".

Back to Dixit & Pindyck book's comments

Hysteresis in Economics:

The firm's status (if is active or if is idle) in the economy is path dependent, for a range of the firm's output price. This concept is important at firm level (entry & exit models) and also at macroeconomic level, in the studies of the aggregated investment from a specific sector of the economy, and sectorial policies.
When considering an investment and abandonment (entry & exit) together, the firm's optimal decision is characterized by two thresholds: one firm's output high price level, when the firm invests in production, and one low price level, when the firm abandon the project. Now suppose the current level of the price is somewhere between these two threshold: What's the status of the firm? Depend of the recent prices' fluctuations history. If the price descended from a high level that induced entry to many competitive firms, then the firm's status remain active. However, if the actual intermediate level was recently preceded by a low prices' level (that induced exit) then the firm remain idle. Or, as pointed out by the book, "the current state of the stochastic variable is not enough to determine the outcome in the economy; a longer history is needed. The economy is path dependent".

Back to Dixit & Pindyck book's comments

Dynamic or Expanded NPV:

This expression has been employed by Trigeorgis in several papers, but the concept can be employed also to refer the NPV calculus in Dixit & Pindyck's Chapter 2.
As Trigeorgis points out,
Expanded (dynamic) NPV = static NPV + Option Premium
The "Option Premium" can be from the (most) relevant option, or a "Combined Option Value" (in a multi-options interactions context). In large companies, with a large project opportunities portfolio, the different "synergy effect" in each portfolio combination, can be added to the above expression, if relevant.

Back to Dixit & Pindyck book's comments

The "bad news principle":

In a world with uncertainty , a "good" project (with positive net present value) can be postponed if a firm can wait to invest, because of the "bad news principle": there is a positive probability of a downward price movement, so that the waiting avoids the possibly losses from the project investment. The threshold price (that warrants immediate investment) depends of the size of the downward movement (not of the upward movement size) and the probability (besides the investment cost, of course), as shown in the equation 16, p.41.
This "bad news principle" was first pointed out by Bernanke, 1983 ("Irreversibility, Uncertainty, and Cyclical Investment", Quarterly Journal of Economics, 98, February 1983, pp.85-106), and some ideas can also be found in Cukierman, 1980 ("The Effects of Uncertainty on Investment under Risk Neutrality with Endogenous Information" ).
A nice and instructive argument is presented by Dixit, 1992 (Investment and Hysteresis, Journal of Economic Perspectives, vol.6, no 1, Winter 1992, pp.107-132, see p.123) illustrating the "bad news principle": Why the Japanese firms (despite its larger fixed costs) are more aggressive investors than the American ones? Because they are protected from the downside risk through the government supports. Then the value of waiting to invest is quite small, because the downside movement potential is small.
For disinvestment (abandon) the argument turns around and becomes the "good news principle": the option value of keeping the operation alive is governed mainly by the upside potential.
See also, in the tutorial page: "The two sides of the uncertainty"

Back to Dixit & Pindyck book's comments

Bellman's Principle of Optimality:

"An optimal policy has the property that, whatever the initial action, the remaining choices constitute an optimal policy with respect to the subproblem starting at the state that results from the initial actions"
(Dixit & Pindyck, 1994, p.100)

Back to Dixit & Pindyck book's comments

Function G(P) Method

This function is defined by the difference of value between the active firm and the idle one (original idea from Dixit, 1989). This function is only defined between the two thresholds (the thick part of the curve). This function helps the comparative statics job, too.
The geometric approach permits a graphical solution for the investment and abandonment thresholds (see footnote at p.220). In a very simple Excel sheet, I performed this method with success: with average of 4 iterations (3 minutes), I got the solution with error less than 0.1 %.

Back to Dixit & Pindyck book's comments

Ex-ante Capacity Choice

In many projects (such as ships, factories, and upstream oil industry) we have an ex ante choice of scale, but prohibitively ex post adjustment in scale. In some situations the optimal is the largest capacity (if there is a increasing returns of scale for the largest scale region), even if is necessary wait for the output price reaches the threshold, and even if the other alternatives' threshold is under the market output price level. In others situations an intermediate scale may be the optimal choice (if there is decreasing returns of scale AND the elasticity of output with respect to investment is also decreasing). In others situations, the optimal is a binary decision between the smallest and the largest scale.
See an excellent exposition of this, with graphical and heuristic argument in the paper of Dixit (1993, Economic Letters, vol.41, pp.265-268).

Back to Dixit & Pindyck book's comments

Back to the Bibliographical Resources

Back to Contents (the main page)