Answer: yes, investing at the threshold line you maximize the option value.
But sometimes you don't lose much investing near of the optimum (instead at the optimum).
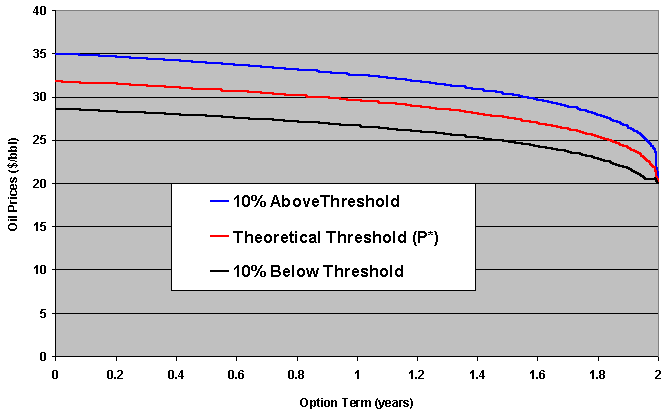
Example: oilfield development as American call option. Suppose oil prices follow a GBM. By running the simple real options model (using "Timing", for example) you draw the theoretical threshold curve.
For example, two sub-optimal option exercise policy are:
The picture below illustrates these sub-optimal thresholds lines.

The option value is calculated by running a Monte Carlo valuation of
these sub-optimal strategies, that is, by generating risk neutral sample
paths for the oil prices evolution and computing the option values
according that threshold line. The option is exercised if the path hit the
sub-optimal threshold (of course the option only can be exercised once for
each sample path).
The expected present value for each sub-optimal strategy is calculated and
compared with the theoretical real option value.
The chart below presents this analysis for sub-optimal strategies, not only for +/- 10% but for several levels of sub-optimal thresholds (% distance from the theoretical optimal threshold).
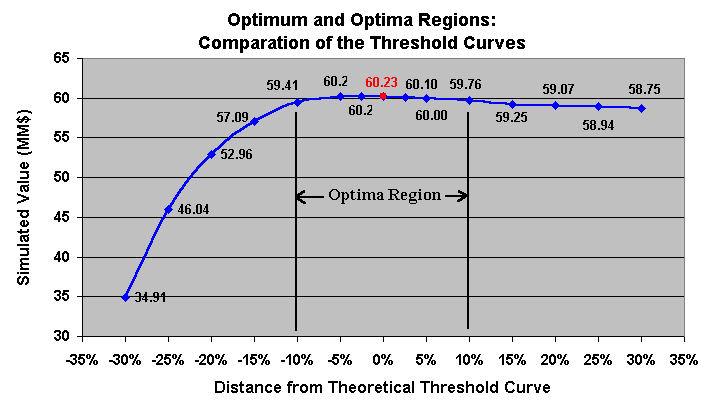
I find out here that the optimum is over a “plateau” (optima region) not a “hill”.
So, investing ~ 10% above or below the theoretical optimum gets rough the same value. But investing ~20% (or more) below the theoretical threshold the losses are very important.
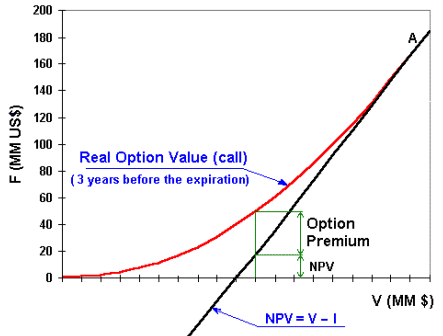
Now the relation optimum with option premium is clear (see the picture below): near of the point A (theoretical threshold) the option premium can be very small, so that investing near of A is sufficient for practical maximization value purposes.
![]()