
Answer: Much better computational efficiency due to good properties such as the lower error for the same number of simulations and the sequential filling in the gaps.
Quasi Monte Carlo approach uses the called low-discrepancy sequences also known as quasi-random sequences. The nice properties of these sequences are studied in the discipline called Number Theory (rather than in Statistics). The basic sequence generates numbers uniformly distributed in the interval [0, 1), replacing the basic pseudo-random numbers (for example the function Rand() in Excel) in simulation applications.
Simulations using the low-discrepancy numbers are called Quasi-Monte Carlo simulations. See much more details at my webpage on Quasi-Monte Carlo simulation.
The following table illustrates the nice statistical properties of quasi-random sequence. It was used a van der Corput sequence in base 2, simulating numbers from a distribution Uniform [0, 1] (see later). The table compare the quasi-random sequence with the (theoretical) Uniform [0, 1] distribution, and with two typical pseudo-random sequences (generate with Excel). In the table,

Hence, quasi-random sequence presents a better performance than typical pseudo-random sequences for all four probabilistic moments, indicating that quasi-random sequence is more representative of U[0, 1] than pseudo-random numbers.
The "filling in the gaps" property is illustrated in the two animations below.
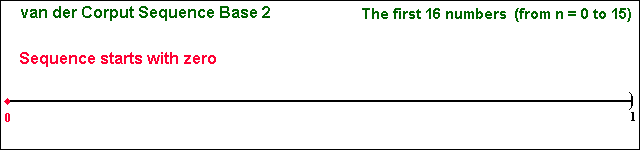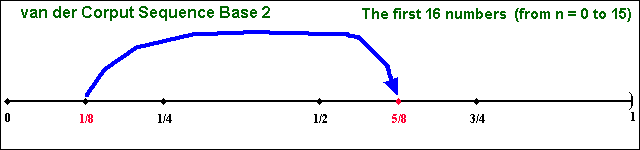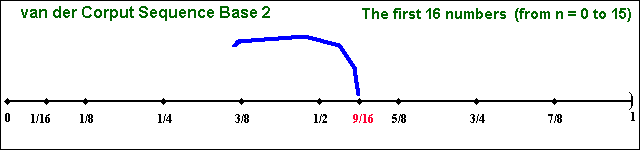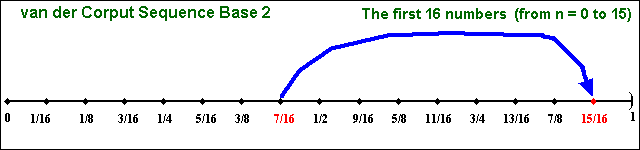
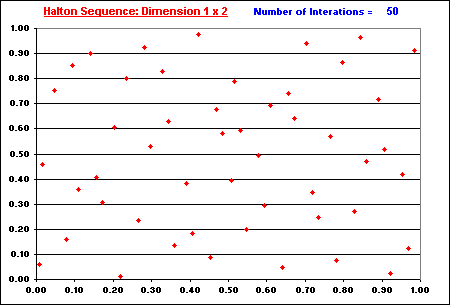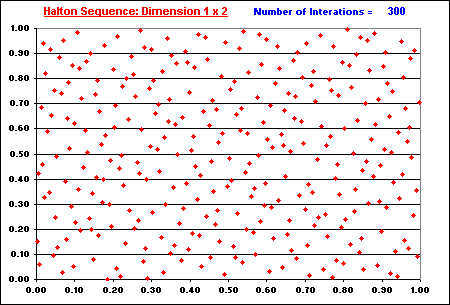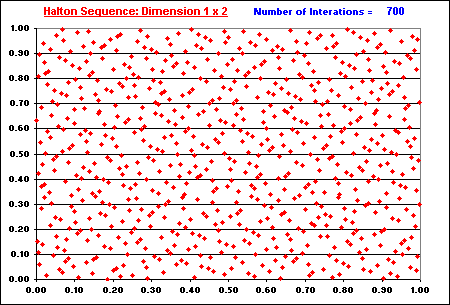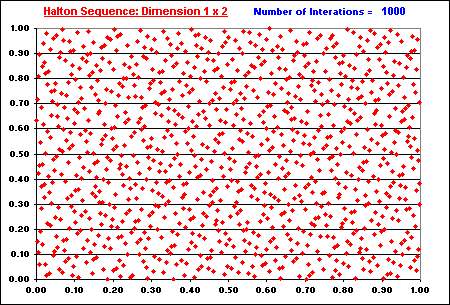
In both animations, the issue of "filling in the gaps" is related to the concept of low-discrepancy, which is associated with the property that the successive numbers are added in a position as away as possible from the others numbers, that is, avoiding clustering (groups of numbers close to other). The sequence is constructed based in the schema that each point is repelled from the others, so that each new point of the sequence is placed so that maximally avoids the other points.
There some problems with the pure quasi-Monte Carlo approach for problems with very high dimensions. But in this case we can use a hybrid quasi-Monte Carlo approach, for example by using random permutations in the quasi-random vectors. See a simple randomization of the quasi-random sequences in my continuation webpage on quasi-Monte Carlo simulation.
For much more additional information, other animations, spreadsheets to download, etc., see the webpage on Quasi-Monte Carlo simulation and the topic Simple Hybrid Quasi-Monte Carlo Approach.
![]()