Last update: January 10th, 2004.
In this section are presented the steps to perform the simulation of the main stochastic processes used in real options applications, that is, the Geometric Brownian Motion, the Mean Reversion Process and the combined process of Mean-Reversion with Jumps.
For all cases I present both simulations the risk-neutral
and the real one.
Risk-neutral simulations are used for derivatives pricing, whereas real simulations are used in other applications like: (a) value at risk; (b) hedging; and, (c) in some real options applications, e.g., to find out the option exercise probability and the waiting expected time before the option exercise (see the Timing spreadsheet).
See the FAQ 4 for a discussion of risk-neutral versus real simulations.
For Web-Browsers that don't understand font "symbol" (like Netscape 6 or higher, but older Netscape versions understand!), the reader can download the pdf version of this page (lower quality for figures and equations): Download the file sim_stoc_proc.pdf with 555 Kb
This webpage includes the topics:
![]() Monte Carlo Simulation of Geometric Brownian Motion
Monte Carlo Simulation of Geometric Brownian Motion
![]() Monte Carlo Simulation of Mean Reversion (Model 1). UPDATED!
Monte Carlo Simulation of Mean Reversion (Model 1). UPDATED!
A new and unprotected Excel spreadsheet is available to download
![]() Complement:
Discretization Accuracy of the
Mean-Reversion Stochastic Process.
Complement:
Discretization Accuracy of the
Mean-Reversion Stochastic Process.
. . . Download an Excel spreadsheet that
simulates this mean-reversion model and discusses the discretization
accuracy.
![]() Monte Carlo Simulation of Mean Reversion (Model 2). UPDATED!
Monte Carlo Simulation of Mean Reversion (Model 2). UPDATED!
![]() A More Practical Approach to Mean Reversion Model 2. .
A More Practical Approach to Mean Reversion Model 2. .
![]() Monte Carlo Simulation of Mean Reversion with Jumps
Monte Carlo Simulation of Mean Reversion with Jumps
. . . Download a spreadsheet
simulating the mean-reversion + jumps sample paths.
![]()
![]() Consider that the price P of a commodity follows a Geometric
Brownian Motion, which is given by the following stochastic equation:
Consider that the price P of a commodity follows a Geometric
Brownian Motion, which is given by the following stochastic equation:
dP = a P dt + s P dz
Where dz = Wiener increment = e dt0.5, e is the standard normal distribution; a is the drift (or capital gain rate); and s is the volatility of P.
By using the equation of total investment return m = a + d, where m is also the risk-adjusted discount rate for P; and d is the dividend yield (or convenience yield in case of commodities). We can rewrite the stochastic equation as:
dP = (m - d) P dt + s P dz
For the risk-neutral version of this equation, just replace the risk-adjusted discount rate m by the risk-free interest rate r to obtain the risk-neutral stochastic equation:
dP = (r - d) P dt + s P dz
Using a logarithm transformation and applying the Itô's
Lemma, we can reach the equations for the prices simulation in both
formats, real and risk-neutral.
For more technical details, see the page on Geometric
Brownian Motion, from the Stochastic Processes section.
The real simulation of a GBM uses the real drift a. The price Pt at the future instant t is given by:
![]()
The simulation of the real prices using the above equation is done by
sampling the standard Normal distribution N(0, 1) and obtaining the
correspondent values for Pt. These values of P can be used to
calculate the (real) values of the project V by means of some equation
V(P) or combined even with other uncertain variables in order to obtain
the real value of V.
Remember, with the real drift simulation of the underlying asset (P), the
required discount rate is the risk-adjusted one m.
Real simulations are used mainly for the calculus of the probability of
option exercise and for the expected time of option exercise (given the option exercises in the simulation), see
the new Timing spreadsheet. In financial
applications, the real simulation is used for VaR (value at Risk)
estimation.
However, for derivatives in general is required other type of simulation,
the risk-neutral one, because the risk-adjusted discount rate for the
derivative F(P) in general is not the same m
used for P.
The risk-neutral simulation of a GBM uses the risk-neutral drift a’ = r - d . The price at t is:
![]()
The simulation of the risk-neutral prices using the above
equation is performed by sampling the standard Normal distribution N(0, 1)
and obtaining the correspondent values for Pt. The
risk-neutral simulation is used mainly for the derivatives valuation in
complete markets. For incomplete markets, is possible use either the
risk-neutral one (but need to select a martingale measure from several or
to estimate the risk-premium in this market) or the real simulation one
with an exogenous risk-adjusted discount rate (dynamic programming), see
FAQ 5.
However, for both the estimation of the probability of option exercise
and the expected time of option exercise, the correct is the real
simulation and not the risk-neutral one.
One important feature of the above discrete-time equations is that the discretization from the continuous-time model is exact. In other words, you don't need to use small time increments Dt in order to get a good approximation. You can use any Dt that the simulation equation is valid (check out this affirmative by evaluating an European call option with time to maturity of one year, for example, by risk-neutral simulation of the underlying asset only at the expiration, and conferring with the exact Black-Scholes formula result).
![]()
Initially consider the following Arithmetic Ornstein-Uhlenbeck process for a stochastic variable x(t):
![]()
This means that there is a reversion force over the
variable x pulling towards an equilibrium level
![]() ,
like a spring force.
,
like a spring force.
The velocity of the reversion process is given by the
parameter h.
This stochastic differential equation is explicitly solvable (see Kloeden & Platen, 1992, topic 4.4, eq.4.2) and has the following solution in terms of stochastic integral (Itô's integral):
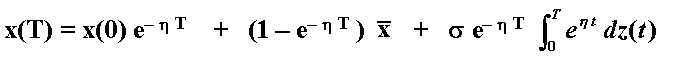
The variable x(T) has Normal distribution with the following expressions for the mean and variance (see for example Dixit & Pindyck, 1994, chapter 3):
![]()
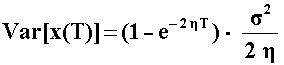
In the expected value equation note that the mean is just a weighted
average between the initial level x(0) and the long-run level
![]() (the weights sum one and are functions of the time and the reversion
speed).
(the weights sum one and are functions of the time and the reversion
speed).
The variance increases with the time, but it also converges to
s2/(2h)
as the time goes to infinite. See the textbook of Oksendal ("Stochastic
Differential Equations - An Introduction with Applications") for
details on Itô's stochastic integration, and the exercise (with
answer) for the mean-reversion process.
There is the following relation between the mean-reversion speed (h)
and the half-life (H) of the process: H = ln(2)/h
(click here for the proof). Half-life is the
time that is expected time for the stochastic variable x to reach the half of the
way toward the equilibrium level ![]() .
.
In order to perform the simulation is necessary to get the discrete-time equation for this process. The correct discrete-time format for the continuous-time process of mean-reversion is the stationary first-order autoregressive process, AR(1), see Dixit & Pindyck, 1994, p.76 (for Dt = 1; the equation below is more general). So the sample path simulation equation for x(t) is performed by using the exact (valid for large Dt) discrete-time expression:
![]()
Schwartz (1997, footnote 15) also recognizes the existence of an "exact
transition equation", but in the last term he uses an
approximation to the variance instead the exact one presented in Dixit &
Pindyck.
Note that the equation above can be viewed as the sum of the expected
value equation with a random term (appear the standard Normal
distribution) with zero mean.
The discretization alternatives with either the first-order Euler's
approximation or the Milstein's approximation formats introduce
discretization errors into the simulation and have higher computational
cost because need small Dt.
The AR(1) discretization presented above is exact in the sense that we can
use large Dt without any problem in terms of
simulation accuracy. See more details in the specific topic below.
Note that x(t) has Normal distribution and can assume even negative
values. In many applications we want that the stochastic variable assume
only positive values, for example in the case of price of commodities P.
How build a good mean-reversion model for P? What is the relation between P and our variable x(t)? What is the relation between the long-run level ![]() and a long-run equilibrium level for a commodity price
and a long-run equilibrium level for a commodity price
![]() ?
?
In this Model 1 (the Model 2 is different at this point), we have two important simple concepts. First, the model identifies the long-run
equilibrium level for a commodity price as a very important reference, so that assume that the commodity price P follows a mean-reversion toward an
equilibrium level ![]() given by the equation:
given by the equation:
![]()
Or the long-run equilibrium level for the commodity is simply ![]() = exp(
= exp(![]() ),
which is constant here.
),
which is constant here.
The second concept from this model 1 is to set the prices in a way that the simulated mean become E[P(T)] = exp{E[x(T)]}, that is, the relation between the variables x and P is such that in the simulation we get the following expected value for the commodity price at the instant T:
![]()
The direct process P(t) = exp[x(t)] doesn't work here because the exponential of a Normal distribution adds the half of the variance in the log-normal distribution mean. In order to reach the goal (E[P(T)] = exp{E[x(T)]}), the half of the variance is compensated using the equation:
![]()
Where Var[x(t)] is a deterministic function of time given before.
With the equations above is easy to simulate the real sample
paths for the commodity prices P following a mean-reversion process. Just simulate x(t) by sampling the Normal distribution and using the equation
for x(t) given before. Calculate Var[x(t)] and use the equation above in order to calculate the (simulated) value for P(t). Make this along the path (along the time for every discrete instant t) and for n
simulated paths.
By combining these three equations, you can simulate the real process for P(t) directly with the equation:
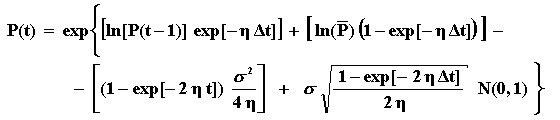
The interpretation for the 4 terms inside the first exp{.} is: (a) the first and second terms are drift terms which weight the initial value and the long-run mean (note that the weights sum 1); (b) the third term is the convex adjustment (or Jensen's inequality adjustment to the drift); and (c) the fourth term is the stochastic term (with the standard Normal), which we sample in the Monte Carlo simulation.
Note also that the volatility parameter enters only in the third and fourth terms, not in the drift, as tell our intuition.
The framework above permits the simulation of the real process. Let us see how to perform the simulation of the risk-neutral mean-reverting process.
Remember that the risk neutral format permits to value derivatives and
requires the use of the risk-free interest rate as the correct discount
rate. As before, the process is risk neutralized by changing the drift. In this risk-neutral format, the drift a of the
process is replaced by r - d, where
d is the dividend yield.
For the mean-reversion case, the real drift is
a = h(![]() -
x), and the dividend yield is not
constant, it is function of x:
-
x), and the dividend yield is not
constant, it is function of x:
d = m - a = m - h(![]() -
x)
-
x)
Where m is the risk-adjusted discount rate
for the underlying asset x (remember the total return is
m = a + d).
With this expression we get the risk-neutral drift for the
mean-reversion process:
r - d
= r - m + h(![]() - x) =
h(
- x) =
h(![]() - x) - (m - r)
= h{[
- x) - (m - r)
= h{[![]() - ((m -r)/h)] - x }
- ((m -r)/h)] - x }
Note that m -r is the
risk-premium. The comparison between both drifts indicates that
the passage from the real process to the risk-neutral one, can be viewed as subtracting the normalized risk-premium (( m - r )/h) from the long run mean level ![]() (= ln
(= ln![]() ).
In other words, in the risk-neutral process the prices revert toward a
level that is lower than the real long-run level, and the subtracting term is a kind of normalized risk-premium.
).
In other words, in the risk-neutral process the prices revert toward a
level that is lower than the real long-run level, and the subtracting term is a kind of normalized risk-premium.
By substituting the risk-neutral drift in the mean-reversion stochastic process, we can reach a slight different equation for the simulation of x(t) and so for P(t).
Hence, the continuous-time risk-neutral stochastic equation for x is given by:
![]()
In the risk-neutral format , the process x(t) is simulated using the exact (valid for large Dt) discrete-time expression:
![]()
The red term is all the difference compared with the real
simulation format (compare with the equation for x(t) presented before).
The process simulation is simple as in the real process case. Calculate x(t) with the equation above and sampling the standard Normal distribution N(0, 1). With the simulated values of x(t), use equation of price P(t) = exp{x(t) - 0.5 Var[x(t)]} together the equation for the variance of x(t) in order to get P(t).
By combining these three equations, you can simulate the risk-neutral process for P(t) directly with the equation:
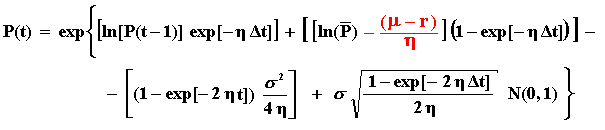
The interpretation of the 4 terms inside the first exp{.} is analogous to the interpretation mentioned for the real simulation (two drift terms, a convex adjustment term, and the stochastic term) but with the drift terms weighting the initial value and the risk-neutral long-run mean instead the real long-run mean.
The spreadsheet below (non-protected) simulate both real and risk-neutral sample-paths of the mean-reversion process described above (Model 1).
![]() Download the Excel spreadsheet
simulation_reversion-model1.xls,
with 45 KB
Download the Excel spreadsheet
simulation_reversion-model1.xls,
with 45 KB
This discretization issue deserves a special discussion. The above
discrete-time equations for the Arithmetic Ornstein-Uhlenbeck x(t) permits
an exact discretization in the sense that the accuracy doesn't decrease if
a larger time-step (Dt) is used.
Because the error from the discretization is eliminated using the above
exact discretization equation, the only error that remains in the
simulation is the error from the random numbers.
This topic discusses the motivation to use a better discretization when
available, including reference to a list of stochastic processes that
permit an exact discretization. This topic also presents an Excel
spreadsheet - available to download, that shows in practice the
superiority of the exact discretization over the popular Euler's
approximation.
The use of large Dt is much more
important in real options (long-term options) than in financial
options - although it is useful also for European financial options.
Perhaps the focus on financial (rather real) options explains why most books ignore the exact simulation equation
for mean-reversion, insisting to teach only Euler and Milstein
approximations even when exact solutions are available.
One exception is the textbook of Kloeden & Platen (1992) that
in the topic 4.4 lists "Some explicitly solvable SDEs".
The Arithmetic Ornstein-Uhlenbeck is their equation 4.2 (for the geometric
Brownian motion, see eq. 4.6 from this textbook). Kloeden & Platen use
the explicitly solvable SDEs (solution doesn't depend on small
Dt) to check the accuracy of numerical methods
that depends on Dt (like Euler
approximations). See pp.308-310 for the geometric Brownian example.
The spreadsheet below simulate this mean-reversion
stochastic process, Model 1, using three different
discretization methods in order to show that the exact method
presented above is the most accurate one.
The spreadsheet also plots the histogram chart (the theoretical is
a log-normal distribution) for the simulated values of the mean-reverting
commodity price at a specified time T and for the other specified
parameters set by the user.
![]() Download the Excel spreadsheet
reversion-simulation_accuracy-vba.xls,
with 372 KB
Download the Excel spreadsheet
reversion-simulation_accuracy-vba.xls,
with 372 KB
The discretization presented before is compared with the popular first order Euler approximation. In short, it uses a discrete time-step Dt substituting directly the differential of time dt. The same is done for the increment dx. The discrete-time version of the Arithmetic Ornstein-Uhlenbeck using the first order Euler's approximation is given by the equation below (see for example the book of Clewlow & Strickland, 2000, p.110, eqs. 7.3 and 7.4):
![]()
As commented before, this equation is less accurate and the accuracy depends of a small time-step Dt. So, with Euler approximation, in addition to the simulation error (from the random numbers), there is the discretization error.
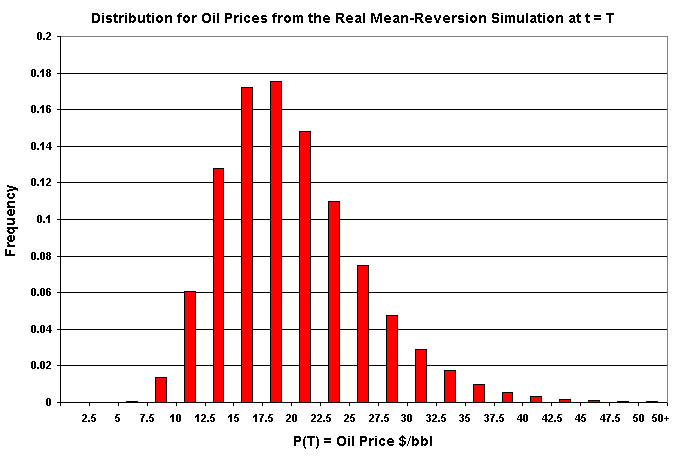
The figure below, a histogram for the oil prices 10 years ahead, was drawn using the spreadsheet above.
![]()
The Model 2 is similar to the model 1 in many aspects, but has important differences. This model is known as "Schwartz Model 1", from his famous paper of 1997 in Journal of Finance (although Schwartz prefers other mean reversion models, e.g., two and three factors models).
The model uses the same equation for x(t) indicated above for the Model 1. The differences are:
In other words there are advantages and disadvantages for this model
when compared with the mean-reversion case analyzed previously (Model 1).
The other advantage of the Schwartz's model is that the application of the Itô's Lemma, in order to get the continuous time stochastic
differential equation for the P(t) process, is easier than model 1.
However, for simulation purposes this step is not necessary (only for the PDE approach is necessary). The correspondent continuous-time stochastic
differential equation for the commodity prices is:
dP = h( ln
![]() - lnP) P dt + s P
dz
- lnP) P dt + s P
dz
This is the Schwartz's eq.1 with other notation. The relation between
![]() and
and ![]() is given by the equation (see the eq. 3 in Schwartz, 1997):
is given by the equation (see the eq. 3 in Schwartz, 1997):
![]() = ln
= ln![]() - (s2/(2h))
- (s2/(2h))
Hence the expected long-run equilibrium price (real process) depends on both the
volatility and the reversion speed.
The real simulation of this model is given by the following equation that again uses an exact discretization that allows large Dt (correcting an old version of this website):
Pt = exp{ [ln(Pt - 1) (exp(-h
Dt))] + [(ln ![]() - (s2/(2h)))
(1 - exp(-h
Dt))] + [s
(SQRT((1- exp(-2h
Dt))/(2h))) N(0,1)] }
- (s2/(2h)))
(1 - exp(-h
Dt))] + [s
(SQRT((1- exp(-2h
Dt))/(2h))) N(0,1)] }
Where the SQRT(.) is the square root operator. The
simulation again is very simple, you get the sample paths of P(t) by
sampling the Normal distribution. and using the equation above.
The expected value for P(t) in the simulation is given by
taking the expectations (including the convexity adjustment) in the above equation:
E[Pt] = exp{ [ln(Pt - 1)
(exp(-h Dt))] +
[(ln ![]() - (s2/(2h))
(1 - exp(-h
Dt))] + [(s2/(4h))
(1 - exp(-2h
Dt))] }
- (s2/(2h))
(1 - exp(-h
Dt))] + [(s2/(4h))
(1 - exp(-2h
Dt))] }
In the long-run (large t), the real simulation converge to the following expected long-run level:
F = E[P(![]() )] = Expected Long-Run Futures Price = exp[
)] = Expected Long-Run Futures Price = exp[![]() + (s2/(4h))] = exp[ln
+ (s2/(4h))] = exp[ln![]() - (s2/(4h))] =
- (s2/(4h))] = ![]() exp[- s2/(4h)]
exp[- s2/(4h)]
For the risk-neutral simulation, just
subtract from ![]() (here = ln
(here = ln ![]() - s2/[2h])
the normalized risk-premium (m - r )/h,
that is, the risk-neutral equation is given by:
- s2/[2h])
the normalized risk-premium (m - r )/h,
that is, the risk-neutral equation is given by:
Pt = exp{ [ln(Pt - 1) (exp(-h
Dt))] + [(ln ![]() - (s2/(2h)
- ((m
- r )/h)) (1 -
exp(-h Dt))] + [s
(SQRT((1- exp(-2h
Dt))/(2h))) N(0,1)] }
- (s2/(2h)
- ((m
- r )/h)) (1 -
exp(-h Dt))] + [s
(SQRT((1- exp(-2h
Dt))/(2h))) N(0,1)] }
If you take expectation of the above equation you get the Schwartz's eq.7 for the expected value of the futures prices in the risk-neutral format (or "under martingale measure", as Schwartz prefers) because the random term (the last one inside the exponential operator) has zero mean (from standard Normal distribution) and considering the convexity adjustment.
On similar way, the expected commodity price in the risk-neutral simulation converges in the long-run (very large t) to the following equation (compare with Schwartz eq. 38):
Expected Long-Run Risk-Neutral Futures Price = exp[![]() - ((m - r )/h)
+ (s2/(4h))]
- ((m - r )/h)
+ (s2/(4h))]
See more about the differences between risk-neutral process and real drift process for the mean-reversion case in the FAQ13.
However, I prefer the model 1 than model 2 because is simpler to see where the simulation is converging, and the formula of prices expectation
is also simpler.
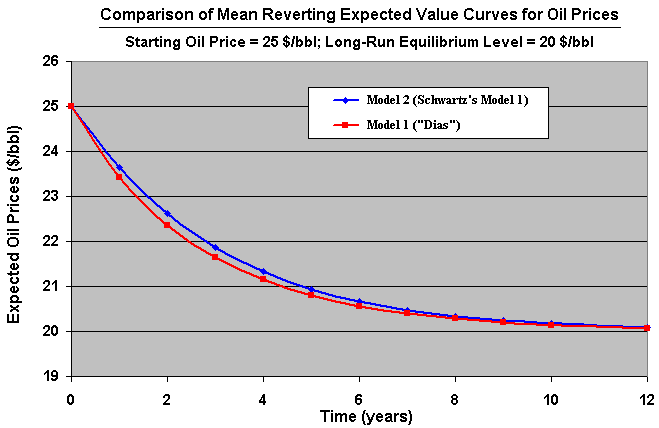
Anyway, simulations has been showing (from a PUC-Petrobras project) that the real options results are very similar for the two models if both
models are simulated with the same long-run level of convergence (by making the Schwartz's long-run futures price equal our Model 1 long-run equilibrium ![]() ) and the same reversion speed h, for example as in the chart below.
) and the same reversion speed h, for example as in the chart below.
F = E[P(![]() )] = Expected Long-Run Futures Price = exp[ln
)] = Expected Long-Run Futures Price = exp[ln![]() - (s2/(4h))] =
- (s2/(4h))] = ![]() exp[- s2/(4h)]
exp[- s2/(4h)]
The practical idea for the user is: instead using the equilibrium level ![]() as input, we enter as input the expected long-run futures price that the simulation converges. So, the equilibrium value is found by inverting the above formula:
as input, we enter as input the expected long-run futures price that the simulation converges. So, the equilibrium value is found by inverting the above formula:
![]() = exp[lnF + (s2/(4h))] = F exp[s2/(4h)]
= exp[lnF + (s2/(4h))] = F exp[s2/(4h)]
Alternatively, we estimate ![]() with a regression (see the page on stochastic processes) or other methods, but we report to managers the value which the real simulation converges (F), which is much more relevant in practice than
with a regression (see the page on stochastic processes) or other methods, but we report to managers the value which the real simulation converges (F), which is much more relevant in practice than ![]() in the Schwartz's model.
in the Schwartz's model.
In this way, the simulation equation for the real prices process is given by:
Pt = exp{ [ln(Pt - 1) (exp(-h Dt))] + [(ln F - (s2/(4h))) (1 - exp(-h Dt))] + [s (SQRT((1- exp(-2h Dt))/(2h))) N(0,1)] }
Where the input F has the managerial meaning of average long-run level that the simulation converges.
For the risk-neutral simulation, the equation using F as input is obtained easily: just subtract from ln F the normalized risk-premium in a similar way done before. This is left as exercise for the reader.
![]()
This model, which I call Marlim Model (reference to
Marlim, the top producer oilfield in Brazil), uses the first
mean-reversion model presented before, but with the addition of random
jumps - modeled with a Poisson process. In addition, jumps are of random
size. The jump process dq is assumed to be independent of the continuous
stochastic increment dz.
Initially consider the following Arithmetic Ornstein-Uhlenbeck process
with discrete jumps (modeled as a Poisson process) for a stochastic
variable x(t):
![]()
This means that there is a reversion force over the variable x pulling
towards an equilibrium level ![]() ,
like a spring force. The velocity of the reversion process is given by the
parameter h. Jumps are represented by the term
dq, which most of time is zero and sometimes occur jumps of uncertain size
f and with arrival rate l.
,
like a spring force. The velocity of the reversion process is given by the
parameter h. Jumps are represented by the term
dq, which most of time is zero and sometimes occur jumps of uncertain size
f and with arrival rate l.
dq = 0 with probability 1 - l dt
dq = f with probability l dt
The jump process dq is assumed independent of dz, the Wiener
increment from the continuous process. That is, the Poisson process is
independent of the mean-reverting process.
The uncertain size of the jumps are modeled with the probability
distribution f. In the classic paper of Merton
(1976) of a jump-diffusion process, the jump-size distribution is assumed
log-normal.
Here is allowed the possibility of both jumps-up and jumps-down, given
that a jump occurred.
Things are easier if we assume that there is the same probability of
jump-up and jump-down, that is, with a frequency l/2 occurs jump-up and
with a frequency l/2 occurs jump-down.
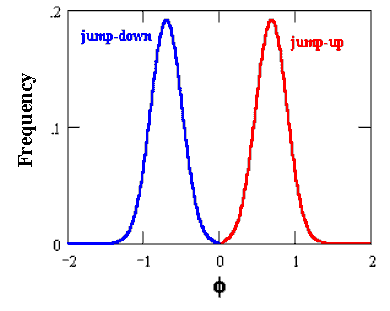
Let assume the following symmetric distributions for the jumps-up
and jumps-down: a two Normal (truncated at zero, at least), with expected
values of ln(2) (= 0.693) in case of jump-up and ln(0.5) (or -ln2) in case
of jump-down. In addition, we assume equal probability for jump-up and
jump-down, so that the expected jump-size is zero (in this case we don't
need to use the compensated
Poisson process, because the expected value of the x(t) is already
independent of the jump). See the figure below.
The variable x(t) has the following expressions for the mean and variance (see for example Das, 1998, Poisson-Gaussian Processes and the Bond Markets) at a future instant T (remember the expected jump-size in this case is zero):
![]()
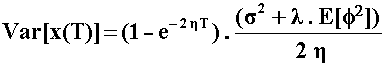
The probability distribution of x(t) is NOT Normal (the jumps adds
fatter tails to the Normal distribution from the mean-reversion
component). For the higher moments expressions, see the previously
mentioned paper of Das (1998).
In the expected value equation again the mean is just a weighted average
between the initial level x(0) and the long-run level
![]() (the
weights sum one). Note that there is no jump term in the expected value
equation. This is the result of our jump model with symmetric
distributions for the jumps up and down AND the 50% probability both jump
directions in case of a jump.
(the
weights sum one). Note that there is no jump term in the expected value
equation. This is the result of our jump model with symmetric
distributions for the jumps up and down AND the 50% probability both jump
directions in case of a jump.
In the variance equation the jump term appear enlarging the variance when
compared with the pure mean-reversion model 1.
It is important to remember that ![]() ,
and in order to obtain this value is necessary to estimate the integral:
,
and in order to obtain this value is necessary to estimate the integral:
![]()
Where f(f) is the probability density function (in the present case the two Normal densities). This integral depends of the distribution f but not of the jump arrival parameter l (so that in practice you can evaluate once the integral, if the jump size distribution is fixed).
The stochastic process for the commodity price P(t)
is chosen so that the commodity prices are function of x(t)
described by the first equation of this item.
First let us to set the following relation between the long run process
mean ![]() and the long-run equilibrium price of the commodity
and the long-run equilibrium price of the commodity
![]() :
:
![]()
The idea is to set the prices in a way that the mean become E[P(T)] = eE[x(T)], that is, the relation between the variable x and P is such that in the simulation we get the following expected value for the commodity price at the instant T:
![]()
The direct process P(t) = ex(t) doesn't work here because the exponential of a normal distribution adds the half of the variance in the log-normal distribution mean. In order to reach the goal (E[P(T)] = eE[x(T)]), the half of the variance is compensated using the equation:
![]()
Where Var[x(t)] is a deterministic function of time, including the jumps contribution, given before in this topic. In the literature (for example Fu et al., 2001), the half-variances of both the continuous process and jump process are subtracted in the simulation equation, but separately.
In the risk-neutral format , the process x(t) is simulated using the discrete-time expression with an appropriate time-step Dt:
![]()
Where m is the risk-adjusted
discount rate for the underlying asset P. The red term (
m - r )/h is the
normalized risk-premium subtracting
the long run mean level ![]() (=
ln(
(=
ln(![]() )).
)).
The simulation process is simple. Calculate x(t) with the equation above,
sampling both the standard Normal distribution N(0, 1) and the possibility
of jump: Poisson process with parameter lup
and ldown for jumps-up and
jumps-down, respectively.
Most of time the Poisson sampling points no jumps (dq = 0), but in case of
jumps, we need to sampling the Normal distributions either for jumps-up or
jumps-down.
Now, with the simulated values of x(t), the simulation of P(t) is easy.
Use equation of price P(t) = exp{x(t) - 0.5
Var[x(t)]} together the equation for the variance of x(t) in order to get
P(t).
The term "jumps" in the equation above adds variance to the x(T) distribution. In case of a deterministic mean-reversion (s = 0) with stochastic jumps, the jumps effect looks significative. The jumps effect on the variance of x(T) that most of time obeys a deterministic mean-reverting process is:
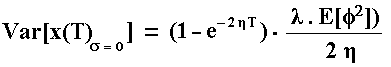
This variance initially grows but stabilizes for very long time T, due to the effect of the mean-reversion force. It is not difficult to see in the above equation that when, in addition to the s = 0, the reversion speed h tends to zero (no mean-reversion) the pure jumps process with random jump-size given by the probability distribution f, has the following variance (take the limit in the last equation):
Var[x(T)pure jumps] = l E[f2] T
Without the mean-reverting force, the variance of jumps grows with the time so that it is not bounded as before.
What is the appropriate time-step Dt?
Although the discretization for the mean-reverting part of the equation of
x(t) is exact (valid for very large Dt), the
presence of jumps together with the reversion creates some problems to use
large Dt. For geometric Brownian process
combined with jumps there is no problem because the process drift doesn't
depend on the current level of the stochastic variable (it is possible
even to use Brownian bridge with independent simulations for each
process). The same is not true for mean-reversion process - the
drift is function of the current value of the stochastic variable. Hence,
the combination of reversion with jumps deserves more caution.
For the case with jumps combined with mean-reversion, I recommend
to use a relatively small Dt, but
larger than the required by Euler and Milstein approximations to reach a
similar accuracy, in most cases.
The idea is as follow. If the time interval Dt
is sufficiently small, the probability of two jumps occurrence is
negligible because (l.Dt)2
is much lower than (l.Dt).
So in this case we can consider only one jump in each time interval.
In order to illustrate the problem, imagine for example a
Dt = 1 year and l
= 1/year. The probability of occurrence of two jumps in one year is given
by P[N(t) = n] = (1/n!) (l t)n e-
l t = 18.4% (make n = 2; l = 1; t
= 1), which is not negligible. If we consider both jumps at the ending of
the year, the mean-reversion will not act through the year, reducing the
jump shocks effect at the ending of the year. A very different result
will occur if one jump is considered at the beginning of the year (so the
reversion will exercise a strong force along the year, and the other one at
the ending of the year.
However, in the oil price process we are interested in rare large jumps
only and we can use smaller time-steps. Assume l
= 0.25 per annum (is expected only one jump each 4 years). By using a
Dt = 1 month (= 0.08 year), the probability of
two jumps in this period (one month) is only 0.02%, which is
negligible (the probability of one jump is > 2% and is not
negligible). In practice this means that we can assume only one jump using
a smaller Dt (as in this case).
Even for the case with jumps associated with the mean-reversion, is
preferable to use the above discretization for x(t) than approximations
for the mean-reverting part using Euler or Milstein approximations. The
Euler or Milstein approximations require very small Dt
even without jumps. With jumps, a Dt of one
month in the above example means a larger error than using the exact
discretization used for the mean-reverting part.
For the real process simulation (instead
the risk-neutral one), use the same equation for x(t) , but without the
normalized risk-premium ( m - r )/h)
subtracting the long run mean level ![]() (=
ln(
(=
ln(![]() )),
that is the real simulation for x(t) is given by:
)),
that is the real simulation for x(t) is given by:
![]()
The Excel spreadsheet available to download below, shows the real and risk-neutral sample-paths from a simulation of the mean-reversion with jumps, named Marlim model (press F9 to get new sample paths in the chart):
![]() Download the Excel spreadsheet
simulation-reversion-jumps-marlim-real_x_rn.xls,
with 235 KB
Download the Excel spreadsheet
simulation-reversion-jumps-marlim-real_x_rn.xls,
with 235 KB
In the spreadsheet, were used a fixed jump-sizes for both jump-up and jump-down. However, it is easy to set probability distributions for the jumps-size. The formulas used in the spreadsheet are the ones presented above.
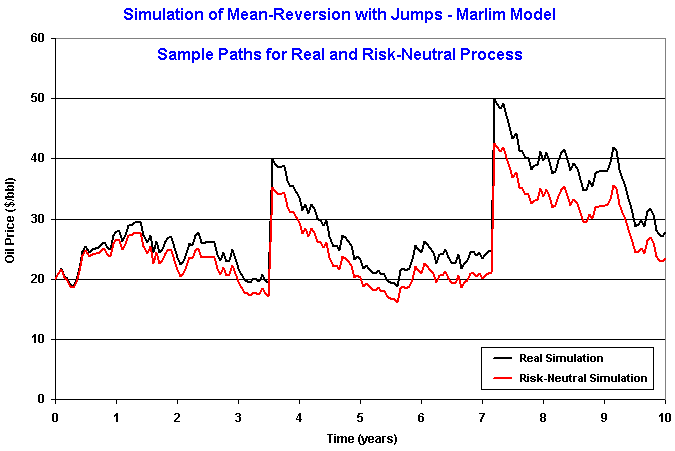
The chart below presents an example of sample paths simulation for both
the real and the risk-neutral simulation of a mean-reversion with jumps,
from the spreadsheet.
In this example the Marlim model considered l
= 0.25 (is expected one jump each 4 years), with equal probability to be
jump-up or jump-down; reversion with half-life of two years towards an
equilibrium level of 20 $/bbl; volatility of 20%, etc (see the spreadsheet
available before for details).
Algorithm: Most Monte Carlo commercial software (such as
@Risk, Crystal Ball, etc.) have direct facilities for simulation of
Poisson distributions. However, some readers could be interested on build
up a simple simulator for Poisson distribution, and it is presented below.
One algorithm for the simulation of jumps occurrence is given by the
following simple procedure based in Dupire's "Monte Carlo Toolkit"
(1998), and it is valid for small Dt (maximum
one jump in this small interval):
Many jumps in a time-interval- If the time interval Dt is sufficiently small, the probability of two jumps occurrence is negligible. However, for large Dt, this is not true: is necessary to consider more than one jump. In this case the jumps term become:
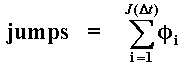
Where J(Dt) ~ Poisson(l.Dt)
gives the number of jumps in this time interval, each of them with
uncertain size fi.
In case of no jumps, in the equation above jumps = 0.
In practical terms, make jumps = jumps-up + jumps-down, so we get two
summations, one for jumps-up and another for jumps-down, each with arrival
rate of l/2 (if jump-up and jump-down have 50%
chances each in case of one jump) and with distributions
fup and fdown,
respectively inside the summations. However, again I recommend a small
Dt so that the probability of more than one
jump is negligible.
In order to consider more than one jump in each time-interval, it is necessary a more general algorithm for Poisson processes. This algorithm is generally based in the relationship between the Poisson(l) distribution and the exponential distribution, expo(1/l), is given in the textbook of Law & Kelton (2000, p.478).
![]()
![]()